 θετικοί πραγματικοί να αποδειχθεί ότι:
θετικοί πραγματικοί να αποδειχθεί ότι: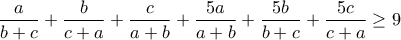
Συντονιστές: achilleas, emouroukos, silouan
Διονύσιος Αδαμόπουλος έγραψε:Ανθετικοί πραγματικοί να αποδειχθεί ότι:
Ορέστη, αυτό το επιχείρημα δεν είναι σωστό. Η αρχική ανισότητα είναι κυκλική, αλλά όχι συμμετρική. ως εκ τούτου δεν έχεις δικάιωμα να θεωρήσεις ότι δεν βλάπτεται η γενικότητα λέγονταςΟρέστης Λιγνός έγραψε: Αυτή γράφεται.
Έστω χωρίς βλάβη.

δεν ισχύει, όπως θα διαπιστώσεις αν θέσειςΟρέστης Λιγνός έγραψε: ...που ισοδυναμεί με.
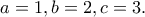

 , οπότε υπάρχουν
, οπότε υπάρχουν  ώστε
ώστε 

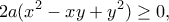 αρκεί να αποδείξουμε ότι
αρκεί να αποδείξουμε ότι  .
. αυτή ισχύει. Διαφορετικά, διαιρώντας με
αυτή ισχύει. Διαφορετικά, διαιρώντας με  και θέτοντας
και θέτοντας  έχουμε να αποδείξουμε ότι
έχουμε να αποδείξουμε ότι . Στο σημείο αυτό θα μπορούσαμε να συνεχίσουμε με λόγισμό (η συνάρτηση έχει θετική ελάχιστη τιμή στο διάστημα
. Στο σημείο αυτό θα μπορούσαμε να συνεχίσουμε με λόγισμό (η συνάρτηση έχει θετική ελάχιστη τιμή στο διάστημα  ).
). ![\displaystyle{t^3+2t^2+1=t^3+t^2+t^2+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\stackrel{AM-GM}{\geq }7\sqrt[7]{\frac{t^7}{4^4}}=\frac{7}{\sqrt[7]{4^4}}t} \displaystyle{t^3+2t^2+1=t^3+t^2+t^2+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\stackrel{AM-GM}{\geq }7\sqrt[7]{\frac{t^7}{4^4}}=\frac{7}{\sqrt[7]{4^4}}t}](/forum/ext/geomar/texintegr/latexrender/pictures/bfeb0dabcd1ba55dc51e74f357ee1fad.png) .
.![\displaystyle{\frac{7}{\sqrt[7]{4^4}}>3} \displaystyle{\frac{7}{\sqrt[7]{4^4}}>3}](/forum/ext/geomar/texintegr/latexrender/pictures/c95d053641036028b86b8c01724be770.png) . Αυτό βλέπουμε ότι ισχύει, αφού οι γίνουν οι πράξεις ρουτίνας.
. Αυτό βλέπουμε ότι ισχύει, αφού οι γίνουν οι πράξεις ρουτίνας.Μεταφέρθηκε στους Seniors.matha έγραψε:Βάζω μια απόδειξη για την ανισότητα, από την οποία φαίνεται ότι το θέμα δεν απευθύνεται σε junior μαθητές.
Μέχρι αυτό το σημείο συμφωνεί και η δικιά μου λύση. Από αυτό το σημείο και μετά:matha έγραψε:
Αρκεί να αποδείξουμε ότι
 είναι
είναι  ή
ή  , τότε η ανισότητα ισχύει με ισότητα όταν
, τότε η ανισότητα ισχύει με ισότητα όταν  (όταν δηλαδή οι
(όταν δηλαδή οι  είναι ίσοι).
είναι ίσοι).  αν
αν  διαφορετικοί θετικοί πραγματικοί.
διαφορετικοί θετικοί πραγματικοί. , τότε έχουμε ότι:
, τότε έχουμε ότι: 
 , τότε η ανισότητα μπορεί να γίνει
, τότε η ανισότητα μπορεί να γίνει  και θέτουμε
και θέτουμε  , όπου
, όπου  .
. 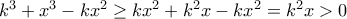

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες