 ισχύουν
ισχύουν  και
και 
Να βρεθεί το μέγιστο του αθροίσματος

Συντονιστές: achilleas, emouroukos, silouan
 ισχύουν
ισχύουν  και
και 


 και
και  οπότε από την υπόθεση είναι
οπότε από την υπόθεση είναι 
 να είναι ομόσημοι. Δίχως βλάβη της γενικότητας, υποθέτουμε ότι
να είναι ομόσημοι. Δίχως βλάβη της γενικότητας, υποθέτουμε ότι  και
και  Τότε, είναι
Τότε, είναι  και
και 



 Αν
Αν  τότε
τότε  και
και  κι επομένως
κι επομένως




 Αν
Αν  τότε
τότε  και
και  οπότε
οπότε






![\displaystyle{ \Leftrightarrow \left( {b + 2} \right)\left( {c + 2} \right)\left[ {\left( {b - 2} \right)\left( {c - 2} \right) - \left( {b + 2} \right)\left( {c + 2} \right)} \right] \ge 0 \Leftrightarrow } \displaystyle{ \Leftrightarrow \left( {b + 2} \right)\left( {c + 2} \right)\left[ {\left( {b - 2} \right)\left( {c - 2} \right) - \left( {b + 2} \right)\left( {c + 2} \right)} \right] \ge 0 \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/f302e75b7c5873afc9bacd1655170ca3.png)

 ή
ή 
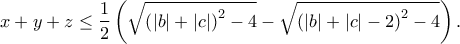
 με
με  Για
Για  είναι
είναι
 που είναι αδύνατο. Άρα, η
που είναι αδύνατο. Άρα, η  διατηρεί πρόσημο στο
διατηρεί πρόσημο στο  κι αφού
κι αφού  θα είναι
θα είναι  για κάθε
για κάθε  Άρα, η
Άρα, η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  οπότε
οπότε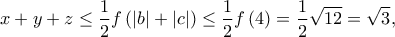
 οπότε και
οπότε και  Στην περίπτωση αυτή είναι
Στην περίπτωση αυτή είναι  και
και 
 είναι ίση με
είναι ίση με  και λαμβάνεται για την τριάδα
και λαμβάνεται για την τριάδα 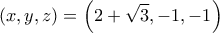 καθώς και τις μεταθέσεις της.
καθώς και τις μεταθέσεις της.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες