 θετικός ακέραιος και
θετικός ακέραιος και  . Να αποδείξετε ότι οι αριθμοί
. Να αποδείξετε ότι οι αριθμοί  ,
,  και
και 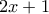 είναι μήκη πλευρών τριγώνου, του οποίου το εμβαδόν και η ακτίνα του εγγεγραμμένου κύκλου είναι επίσης ακέραιοι αριθμοί.
είναι μήκη πλευρών τριγώνου, του οποίου το εμβαδόν και η ακτίνα του εγγεγραμμένου κύκλου είναι επίσης ακέραιοι αριθμοί.Συντονιστές: achilleas, emouroukos, silouan
 θετικός ακέραιος και
θετικός ακέραιος και  . Να αποδείξετε ότι οι αριθμοί
. Να αποδείξετε ότι οι αριθμοί  ,
,  και
και 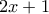 είναι μήκη πλευρών τριγώνου, του οποίου το εμβαδόν και η ακτίνα του εγγεγραμμένου κύκλου είναι επίσης ακέραιοι αριθμοί.
είναι μήκη πλευρών τριγώνου, του οποίου το εμβαδόν και η ακτίνα του εγγεγραμμένου κύκλου είναι επίσης ακέραιοι αριθμοί.Ας είναιemouroukos έγραψε:Έστωθετικός ακέραιος και
. Να αποδείξετε ότι οι αριθμοί
,
και
είναι μήκη πλευρών τριγώνου, του οποίου το εμβαδόν και η ακτίνα του εγγεγραμμένου κύκλου είναι επίσης ακέραιοι αριθμοί.

 και
και 
 .
. και ισχύει προφανώς
και ισχύει προφανώς  .
. όπου
όπου  .
. ισχύει
ισχύει .
. .
.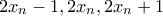 είναι πλευρές τριγώνου, αφού ισχύει
είναι πλευρές τριγώνου, αφού ισχύει  )
) άρα όλοι οι όροι είναι θετικοί ακέραιοι.
άρα όλοι οι όροι είναι θετικοί ακέραιοι.
 (
( ).
). και ακόμα είναι
και ακόμα είναι  .
. ).
).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες