
και

Να αποδείξετε ότι :
 \displaystyle{\frac{1}{\sqrt{x_{2}}} + ... +}
\displaystyle{\frac{1}{\sqrt{x_{2}}} + ... +}
Συντονιστές: achilleas, emouroukos, silouan


 \displaystyle{\frac{1}{\sqrt{x_{2}}} + ... +}
\displaystyle{\frac{1}{\sqrt{x_{2}}} + ... +}
 για
για  Τότε είναι
Τότε είναι  οπότε για κάθε
οπότε για κάθε  ισχύει:
ισχύει:

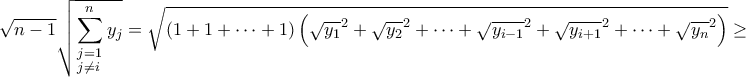






 , προκύπτει ότι:
, προκύπτει ότι:

 μπορεί να είναι
μπορεί να είναι  .
.


 φθίνουν ενώ τα
φθίνουν ενώ τα  αυξάνουν
αυξάνουν )
)Τέλεια! Μπορούμε να την φτιάξουμε ώστε να δουλεύει και γιαΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Θα δώσω μία λύση για την ειδική περίπτωση που
Να σημειώσω ότι μόνο τομπορεί να είναι
.
Η ανισότητα γράφεται
Αλλά
Εχουμε
γιατί ταφθίνουν ενώ τα
αυξάνουν
(στο τελευταίο χρειάζεται το)
οπότε αποδείχθηκε.
 . Αντί να χρησιμοποιήσουμε την ανισότητα Chebychev θα χρησιμοποιήσουμε την απόδειξή της:
. Αντί να χρησιμοποιήσουμε την ανισότητα Chebychev θα χρησιμοποιήσουμε την απόδειξή της: παίρνουμε
παίρνουμε  για κάθε
για κάθε  με
με  . Άρα
. Άρα  ή ισοδύναμα
ή ισοδύναμα  .
.

 . (Για
. (Για  είναι προφανές ενώ για
είναι προφανές ενώ για  επειδή
επειδή  .)
.)Η παραπάνω απόδειξη μπορεί να συμπληρωθεί ως εξής:ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Θα δώσω μία λύση για την ειδική περίπτωση που
Να σημειώσω ότι μόνο τομπορεί να είναι
.
Η ανισότητα γράφεται
Αλλά
Εχουμε
γιατί ταφθίνουν ενώ τα
αυξάνουν
(στο τελευταίο χρειάζεται το)
οπότε αποδείχθηκε.
 και παρατηρούμε ότι
και παρατηρούμε ότι  για κάθε
για κάθε 

 τότε
τότε  και άρα, αφού η
και άρα, αφού η 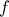 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  θα είναι
θα είναι 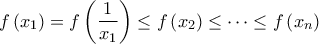
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες