
Θέτουμε

Να δειχθεί ότι

Συντονιστές: achilleas, emouroukos, silouan
 θέτω
θέτω  Για
Για  και ακέραιο
και ακέραιο  έχω
έχω![\displaystyle{ x + 2C_k = \frac{x}{k-1} + \cdots + \frac{x}{k-1} + C_k + C_k \geqslant (k+1)\left[ \frac{x^{k-1}}{(k-1)^{k-1}} C_k^2\right]^{1/(k+1)} = x^{(k-1)/(k+1)}} \displaystyle{ x + 2C_k = \frac{x}{k-1} + \cdots + \frac{x}{k-1} + C_k + C_k \geqslant (k+1)\left[ \frac{x^{k-1}}{(k-1)^{k-1}} C_k^2\right]^{1/(k+1)} = x^{(k-1)/(k+1)}}](/forum/ext/geomar/texintegr/latexrender/pictures/713f87ccfb033cfb03c4ddd9f0fa24b7.png)
 έχω
έχω  ή ισοδύναμα
ή ισοδύναμα
 . Επίσης ισχύει και για
. Επίσης ισχύει και για  αν θέσουμε
αν θέσουμε  .
.


 . Η ανισότητα ισχύει και για
. Η ανισότητα ισχύει και για  . Οπότε τηλεσκοπικά είναι
. Οπότε τηλεσκοπικά είναι 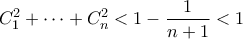
 μπροστά από την ρίζα βελτιώνεται κάπως.
μπροστά από την ρίζα βελτιώνεται κάπως.
 .Αν είναι
.Αν είναι  δεν υπάρχει κανένα πρόβλημα.
δεν υπάρχει κανένα πρόβλημα.
 τότε
τότε 
 τότε
τότε 

 .Αυτή είναι εκείνο το
.Αυτή είναι εκείνο το  που ελαχιστοποιεί το φράγμα που βρήκαμε.Ελαχιστοποιούμε την συνάρτηση αυτή ως προς
που ελαχιστοποιεί το φράγμα που βρήκαμε.Ελαχιστοποιούμε την συνάρτηση αυτή ως προς 
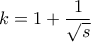
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες