Αρκεί να αποδειχθεί ότι το σημείο

, ταυτίζεται με το αντιδιαμετρικό σημείο του

και άρα, αρκεί να αποδειχθεί ότι

.
Έστω

, το αντιδιαμετρικό σημείο του

και από

, αρκεί να αποδειχθεί ότι

λόγω του ορθογωνίου τριγώνου

.
Από

και

, λόγω

, αρκεί να αποδειχθεί ότι ισχύει

Από

αρκεί να αποδειχθεί ότι η ευθεία

εφάπτεται στον περίκυκλο έστω

του τριγώνου

.
Αυτό όμως αληθεύει.

- Καθετότητα και παραλληλία.
- f=185_t=55835.PNG (42 KiB) Προβλήθηκε 1570 φορές
Πράγματι, από το εγγράψιμο τετράπλευρο

, όπου

και το ορθογώνιο τρίγωνο

, με

, έχουμε
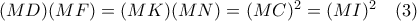
λόγω

( γνωστό αποτέλεσμα ).
Συμπεραίνεται έτσι,


, με

και το ζητούμενο έχει αποδειχθεί.
Κώστας Βήττας.
ΥΓ. Η παραλληλία

είναι ένα πρόσθετο αποτέλεσμα προς απόδειξη, το οποίο όμως δεν είναι χρειαζούμενο στα δοσμένα της εκφώνησης , αλλά ούτε απαραίτητο για την απόδειξη του ζητούμενου.
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  (κέντρου
(κέντρου  ,
,  ο εγγεγραμμένος του κύκλος και
ο εγγεγραμμένος του κύκλος και  το σημείο επαφής του
το σημείο επαφής του  με την
με την  .
.  με
με  το μέσο του τόξου
το μέσο του τόξου  που δεν περιέχει την κορυφή
που δεν περιέχει την κορυφή  και
και  να δειχθεί ότι
να δειχθεί ότι  με
με  το κέντρου του
το κέντρου του  παρεγγεγραμμένου κύκλου του τριγώνου και
παρεγγεγραμμένου κύκλου του τριγώνου και  και
και

 , ταυτίζεται με το αντιδιαμετρικό σημείο του
, ταυτίζεται με το αντιδιαμετρικό σημείο του  .
. , το αντιδιαμετρικό σημείο του
, το αντιδιαμετρικό σημείο του  , αρκεί να αποδειχθεί ότι
, αρκεί να αποδειχθεί ότι  λόγω του ορθογωνίου τριγώνου
λόγω του ορθογωνίου τριγώνου  .
. και
και  , λόγω
, λόγω  , αρκεί να αποδειχθεί ότι ισχύει
, αρκεί να αποδειχθεί ότι ισχύει 
 αρκεί να αποδειχθεί ότι η ευθεία
αρκεί να αποδειχθεί ότι η ευθεία  εφάπτεται στον περίκυκλο έστω
εφάπτεται στον περίκυκλο έστω  του τριγώνου
του τριγώνου  .
. , όπου
, όπου  και το ορθογώνιο τρίγωνο
και το ορθογώνιο τρίγωνο  , με
, με  , έχουμε
, έχουμε 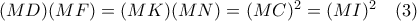 λόγω
λόγω  ( γνωστό αποτέλεσμα ).
( γνωστό αποτέλεσμα ).
 , με
, με  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Έστω το σημείο
Έστω το σημείο  και αρκεί ως ισοδύναμο ζητούμενο, να αποδειχθεί ότι ταυτίζεται με το σημείο επαφής του κύκλου
και αρκεί ως ισοδύναμο ζητούμενο, να αποδειχθεί ότι ταυτίζεται με το σημείο επαφής του κύκλου  στην
στην  και το ορθογώνιο τρίγωνο
και το ορθογώνιο τρίγωνο  λόγω
λόγω  .
.
 εφάπτεται στον περίκυκλο έστω
εφάπτεται στον περίκυκλο έστω  του τριγώνου
του τριγώνου  και επομένως, ισχύει
και επομένως, ισχύει 
 λόγω
λόγω  .
.



 λόγω
λόγω  και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί. Τα σημεία
Τα σημεία  παραμένουν αμετάβλητα και ο κύκλος
παραμένουν αμετάβλητα και ο κύκλος  γίνεται η ευθεία
γίνεται η ευθεία  Εφόσον
Εφόσον  το
το  πηγαίνει στο
πηγαίνει στο  με την πλευρά
με την πλευρά 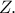 Επειδή
Επειδή  έπεται πως
έπεται πως 


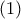 και
και  προκύπτει πως
προκύπτει πως 




 συμπεραίνουμε ότι αρκεί
συμπεραίνουμε ότι αρκεί 
![\displaystyle \Longleftrightarrow 2\cos \frac{B}{2}\left [ \cos \frac{C}{2}\cos \left ( \frac{B}{2}+\frac{C}{2} \right )+\sin \frac{C}{2}\sin \left ( \frac{B}{2}+\frac{C}{2} \right ) \right ]=1+\cos B \Longleftrightarrow \displaystyle \Longleftrightarrow 2\cos \frac{B}{2}\left [ \cos \frac{C}{2}\cos \left ( \frac{B}{2}+\frac{C}{2} \right )+\sin \frac{C}{2}\sin \left ( \frac{B}{2}+\frac{C}{2} \right ) \right ]=1+\cos B \Longleftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/cc27667b873cbc6e40fff6c4a1cf4561.png)
 που αληθεύει.
που αληθεύει. 
 που ολοκληρώνει την απόδειξη.
που ολοκληρώνει την απόδειξη.