Σε τρίγωνο
 να αποδειχθεί ότι
να αποδειχθεί ότι 
Συντονιστές: vittasko, silouan, Doloros
 να αποδειχθεί ότι
να αποδειχθεί ότι 
Καλησπέρα Τηλέμαχε.ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: Σε τρίγωνονα αποδειχθεί ότι
 (βγαίνει εύκολα από τις
(βγαίνει εύκολα από τις 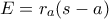 και λοιπά) και την
και λοιπά) και την  . Η τελευταία από τον Νόμο των ημιτόνων παίρνει και την μορφή
. Η τελευταία από τον Νόμο των ημιτόνων παίρνει και την μορφή 
![\displaystyle {3 \sqrt [3] { \frac{abc}{r_{a}r_{b}r_{c}}} \ge 2\sqrt{3} \displaystyle {3 \sqrt [3] { \frac{abc}{r_{a}r_{b}r_{c}}} \ge 2\sqrt{3}](/forum/ext/geomar/texintegr/latexrender/pictures/ab67b28879e1a1888fdecee7c072bdeb.png) .
.![\displaystyle {3 \sqrt [3] { \frac{abc}{r_{a}r_{b}r_{c}}} = 3 \sqrt [3] { \frac{4ER}{Es}} = 3 \sqrt [3] { \frac{4R}{s}} \ge 3 \sqrt [3] { \frac{8}{3\sqrt {3}}} = 2\sqrt{3} \displaystyle {3 \sqrt [3] { \frac{abc}{r_{a}r_{b}r_{c}}} = 3 \sqrt [3] { \frac{4ER}{Es}} = 3 \sqrt [3] { \frac{4R}{s}} \ge 3 \sqrt [3] { \frac{8}{3\sqrt {3}}} = 2\sqrt{3}](/forum/ext/geomar/texintegr/latexrender/pictures/2ba934452700258b174cc3c2682ec937.png) , όπως θέλαμε.
, όπως θέλαμε. 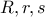 και λοιπά καθώς και τον βασιλιά των ανισοτήτων του τριγώνου,
και λοιπά καθώς και τον βασιλιά των ανισοτήτων του τριγώνου,  .
. 
 , όπως θέλαμε.
, όπως θέλαμε. μήκη πλευρών τριγώνου , τότε οι
μήκη πλευρών τριγώνου , τότε οι  αποτελούν πλευρές τριγώνου με ακτίνα περιγεγραμμένου κύκλου ίση με
αποτελούν πλευρές τριγώνου με ακτίνα περιγεγραμμένου κύκλου ίση με  και με εμβαδόν το μισό του
και με εμβαδόν το μισό του 

 την ανισότητα
την ανισότητα  προκύπτει ότι
προκύπτει ότι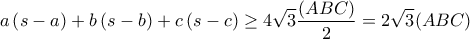
 προκύπτει ότι
προκύπτει ότι 


 και η τελευταία είναι γνωστό ότι ισχύει.
και η τελευταία είναι γνωστό ότι ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες