
Έστω το σημείο

, ως το ορθόκεντρο του τριγώνου

και έστω τα σημεία

και

Από τα όμοια ορθογώνια τρίγωνα

, έχουμε
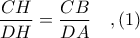
Από τα όμοια ισοσκελή τρίγωνα

, έχουμε

Από
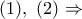

Από

και

, προκύπτει ότι τα τρίγωνα

είναι όμοια.
Στα όμοια αυτά τρίγωνα, οι

είναι ομόλογες ευθείες, λόγω

και άρα έχουμε

Από


και επομένως, αρκεί να αποδειχθεί ότι ισχύει

.

Οι δια των σημείων

, κάθετες ευθείες επί την ευθεία

, τέμνουν τις ευθείες

στα σημεία

αντιστοίχως και σύμφωνα με το παρακάτω
Λήμμα, έχουμε

Από

και

, έχουμε




- Μία καθετότητα που με παίδεψε.
- f=185_t=57304(a).png (52.79 KiB) Προβλήθηκε 1317 φορές

Από

και

, έχουμε ότι το σημείο

ταυτίζεται με το ορθόκενρο του τριγώνου

και άρα έχουμε

και επομένως, ισχύει

με

.
Στο τετράπλευρο

τώρα, ισχύει

λόγω
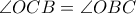
και

και

.
Άρα, το τετράπλευρο

είναι εγγράψιμο σε κύκλο έστω

και επομένως έχουμε
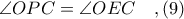
Αλλά,

λόγω των όμοιων ισοσκελών τριγώνων

, με

το μέσον του

και τα σημεία
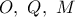
συνευθειακά, λόγω των ισοσκελών τριγώνων

.
Από
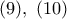
τώρα, προκύπτει ότι το τετράπλευρο

είναι εγγράψιμο και επομένως, ο κύκλος

περνάει από το σημείο

.
Ομοίως, αποδεικνύεται ότι το τετράπλευρο

είναι εγγράψιμο σε κύκλο έστω

, ο οποίος περνάει επίσης από το σημείο

.

Από το εγγράψιμο

, έχουμε

Από το εγγράψιμο

έχουμε

Από


και έστω το σημείο

.
Ομοίως, αποδεικνύεται ότι

και έστω το σημείο

.
Από τα όμοια ορθογώνια τρίγωνα

τώρα, έχουμε

Από


Από

, σύμφωνα με το
Θεώρημα Κούτρα, προκύπτει ότι

Από

και


και το ζητούμενο έχει αποδειχθεί.
ΛΗΜΜΑ. - Δίνεται ημικύκλιο  με διάμετρο
με διάμετρο  και έστω
και έστω  μεταβλητό σημείο. Με βάση το τμήμα
μεταβλητό σημείο. Με βάση το τμήμα  κατασκευάζουμε ισοσκελές τρίγωνο
κατασκευάζουμε ισοσκελές τρίγωνο  , με
, με  . Η δια του σημείου
. Η δια του σημείου  κάθετη ευθεία επί την ευθεία
κάθετη ευθεία επί την ευθεία  , τέμνει την ευθεία
, τέμνει την ευθεία  στο σημείο έστω
στο σημείο έστω  . Αποδείξτε ότι καθώς το σημείο
. Αποδείξτε ότι καθώς το σημείο  μεταβάλλεται επί του
μεταβάλλεται επί του  , το μήκος του τμήματος
, το μήκος του τμήματος  παραμένει σταθερό
παραμένει σταθερό .
Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την απόδειξη που έχω υπόψη μου για το ως άνω
Λήμμα.
 εγγεγραμμένο σε ημικύκλιο
εγγεγραμμένο σε ημικύκλιο  με διάμετρο την πλευρά του
με διάμετρο την πλευρά του  . Με βάσεις τις πλευρές
. Με βάσεις τις πλευρές  , κατασκευάζουμε τα όμοια ισοσκελή τρίγωνα
, κατασκευάζουμε τα όμοια ισοσκελή τρίγωνα  αντιστοίχως και ας είναι τα
αντιστοίχως και ας είναι τα  προς το εξωτερικό μέρος του
προς το εξωτερικό μέρος του  και το
και το  προς το εσωτερικό μέρος αυτού. Αποδείξτε ότι
προς το εσωτερικό μέρος αυτού. Αποδείξτε ότι  , όπου
, όπου  .
.
 και
και . Από τον Ν. Συνημιτόνων λαμβάνουμε
. Από τον Ν. Συνημιτόνων λαμβάνουμε 
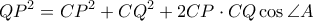 . Επίσης παρατηρούμε ότι
. Επίσης παρατηρούμε ότι 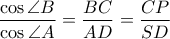 . Συνεπώς ισχύει η ισότητα
. Συνεπώς ισχύει η ισότητα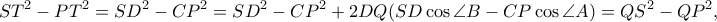 δηλαδή
δηλαδή  .
.
 και ας είναι
και ας είναι  τα σημεία τομής της
τα σημεία τομής της  με τις
με τις  και
και  τα σημεία τομής της
τα σημεία τομής της  με τις
με τις  αντίστοιχα.
αντίστοιχα. στις
στις  τέμνουν αυτές στα σημεία
τέμνουν αυτές στα σημεία  και τις
και τις  στα σημεία
στα σημεία  αντίστοιχα. Τότε θα είναι:
αντίστοιχα. Τότε θα είναι: 


 εγγράψιμα σε κύκλους και με όμοιο τρόπο προκύπτει ότι και
εγγράψιμα σε κύκλους και με όμοιο τρόπο προκύπτει ότι και  είναι επίσης εγγράψιμα σε κύκλους.
είναι επίσης εγγράψιμα σε κύκλους. 




 ύψος του τριγώνου
ύψος του τριγώνου  και με όμοιο τρόπο προκύπτει ότι
και με όμοιο τρόπο προκύπτει ότι  είναι ένα δεύτερο ύψος του άρα το
είναι ένα δεύτερο ύψος του άρα το  ταυτίζεται
ταυτίζεται  .
.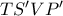 (απέναντι πλευρές του κάθετες στην ίδια ευθεία) προκύπτει ότι
(απέναντι πλευρές του κάθετες στην ίδια ευθεία) προκύπτει ότι 
 .
.
 .
. σύμφωνα με το
σύμφωνα με το
 ή ίσως και κάποιος Pascal να έδειχναν τη συνευθειακότητα των
ή ίσως και κάποιος Pascal να έδειχναν τη συνευθειακότητα των  αλλά αυτά τα «μονοπάτια» τα περπατάει άριστα ο
αλλά αυτά τα «μονοπάτια» τα περπατάει άριστα ο είναι μέσα των
είναι μέσα των  πιθανώς με ευκολότερη απόδειξη. Αναστρέφοντας, βλέπουμε ότι, στην συγκεκριμένη περίπτωση, μπορούμε να γενικεύσουμε αντικαθιστώντας τα μέσα πλευρών με κορυφές όμοιων ισοσκελών τριγώνων. Αυτό βέβαια δεν είναι γενικά δυνατόν, σκεφθείτε πχ το κλασικό αποτέλεσμα της παραλληλίας προς την βάση τριγώνου του ευθύγραμμου τμήματος που ενώνει τα μέσα των δύο πλευρών: δεν μπορούμε να 'ανυψώσουμε' τα δύο αυτά μέσα σε κορυφές όμοιων ισοσκελών τριγώνων. Τι άραγε αλλάζει στο παρόν πρόβλημα (κάνοντας δυνατή την γενίκευση/'ανύψωση');
πιθανώς με ευκολότερη απόδειξη. Αναστρέφοντας, βλέπουμε ότι, στην συγκεκριμένη περίπτωση, μπορούμε να γενικεύσουμε αντικαθιστώντας τα μέσα πλευρών με κορυφές όμοιων ισοσκελών τριγώνων. Αυτό βέβαια δεν είναι γενικά δυνατόν, σκεφθείτε πχ το κλασικό αποτέλεσμα της παραλληλίας προς την βάση τριγώνου του ευθύγραμμου τμήματος που ενώνει τα μέσα των δύο πλευρών: δεν μπορούμε να 'ανυψώσουμε' τα δύο αυτά μέσα σε κορυφές όμοιων ισοσκελών τριγώνων. Τι άραγε αλλάζει στο παρόν πρόβλημα (κάνοντας δυνατή την γενίκευση/'ανύψωση'); και
και  είναι παράλληλα στα ύψη του τριγώνου
είναι παράλληλα στα ύψη του τριγώνου  (λόγω του ημικυκλίου) αφού συνδέουν μέσα δύο πλευρών , άρα
(λόγω του ημικυκλίου) αφού συνδέουν μέσα δύο πλευρών , άρα  , συνεπώς το
, συνεπώς το 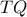 ο φορέας του τρίτου ύψους του εν λόγω τριγώνου
ο φορέας του τρίτου ύψους του εν λόγω τριγώνου 
 (κατά την ίδια φορά) στο επίπεδου του αρχικού τετραπλεύρου (διατηρώντας έτσι τη γωνία τους σταθερή (εν προκειμένου ορθή) καθώς οι κορυφές των (ισοσκελών) τριγώνων απομακρύνονται σε σταθερές διευθύνσεις (κάθετες στις τρεις πλευρές) του αρχικού τετραπλεύρου (εκτός της διαμέτρου του ημικυκλίου) με ανάλογο ρυθμό. !!!!
(κατά την ίδια φορά) στο επίπεδου του αρχικού τετραπλεύρου (διατηρώντας έτσι τη γωνία τους σταθερή (εν προκειμένου ορθή) καθώς οι κορυφές των (ισοσκελών) τριγώνων απομακρύνονται σε σταθερές διευθύνσεις (κάθετες στις τρεις πλευρές) του αρχικού τετραπλεύρου (εκτός της διαμέτρου του ημικυκλίου) με ανάλογο ρυθμό. !!!! , ως το ορθόκεντρο του τριγώνου
, ως το ορθόκεντρο του τριγώνου  και έστω τα σημεία
και έστω τα σημεία  και
και 
 , έχουμε
, έχουμε 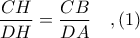
 , έχουμε
, έχουμε 
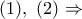

 και
και  , προκύπτει ότι τα τρίγωνα
, προκύπτει ότι τα τρίγωνα  είναι όμοια.
είναι όμοια. είναι ομόλογες ευθείες, λόγω
είναι ομόλογες ευθείες, λόγω  και άρα έχουμε
και άρα έχουμε 

 και επομένως, αρκεί να αποδειχθεί ότι ισχύει
και επομένως, αρκεί να αποδειχθεί ότι ισχύει  .
. , κάθετες ευθείες επί την ευθεία
, κάθετες ευθείες επί την ευθεία  στα σημεία
στα σημεία  αντιστοίχως και σύμφωνα με το παρακάτω
αντιστοίχως και σύμφωνα με το παρακάτω 
 και
και  , έχουμε
, έχουμε 


 και
και  , έχουμε ότι το σημείο
, έχουμε ότι το σημείο  ταυτίζεται με το ορθόκενρο του τριγώνου
ταυτίζεται με το ορθόκενρο του τριγώνου  και άρα έχουμε
και άρα έχουμε 
 με
με  .
. τώρα, ισχύει
τώρα, ισχύει 
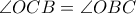 και
και  και
και  .
. και επομένως έχουμε
και επομένως έχουμε 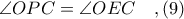
 λόγω των όμοιων ισοσκελών τριγώνων
λόγω των όμοιων ισοσκελών τριγώνων  , με
, με  το μέσον του
το μέσον του  και τα σημεία
και τα σημεία 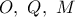 συνευθειακά, λόγω των ισοσκελών τριγώνων
συνευθειακά, λόγω των ισοσκελών τριγώνων  .
.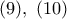 τώρα, προκύπτει ότι το τετράπλευρο
τώρα, προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο και επομένως, ο κύκλος
είναι εγγράψιμο και επομένως, ο κύκλος  είναι εγγράψιμο σε κύκλο έστω
είναι εγγράψιμο σε κύκλο έστω  , ο οποίος περνάει επίσης από το σημείο
, ο οποίος περνάει επίσης από το σημείο  , έχουμε
, έχουμε 


 και έστω το σημείο
και έστω το σημείο  .
. και έστω το σημείο
και έστω το σημείο  .
. τώρα, έχουμε
τώρα, έχουμε 


 , σύμφωνα με το
, σύμφωνα με το 
 και
και 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. μεταβλητό σημείο. Με βάση το τμήμα
μεταβλητό σημείο. Με βάση το τμήμα  κατασκευάζουμε ισοσκελές τρίγωνο
κατασκευάζουμε ισοσκελές τρίγωνο  , με
, με  . Η δια του σημείου
. Η δια του σημείου  κάθετη ευθεία επί την ευθεία
κάθετη ευθεία επί την ευθεία  μεταβάλλεται επί του
μεταβάλλεται επί του  . Η δια του σημείου
. Η δια του σημείου 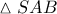 , με
, με  .
. και
και  έχουμε ότι στο τρίγωνο
έχουμε ότι στο τρίγωνο  , το σημείο
, το σημείο 
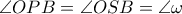 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο και επομένως, έχουμε
είναι εγγράψιμο και επομένως, έχουμε  λόγω
λόγω  .
.
 , προκύπτει ότι το
, προκύπτει ότι το  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. και το
και το