Σκέφτομαι μήπως έχω κουράσει κάποιους με την έμφαση που έχω δώσει...
Σε τρίγωνο
 αποδείξτε ότι
αποδείξτε ότι 
Ζητώ συγνώμη γιατί αρχικά αντί για
 έγραψα
έγραψα 
Συντονιστές: vittasko, silouan, Doloros
 αποδείξτε ότι
αποδείξτε ότι 
 έγραψα
έγραψα 
Καλημέρα Τηλέμαχε.ΚΕΦΑΛΟΝΙΤΗΣ έγραψε:Με τόσα που έχω προτείνει στο παρελθόν σχετικά με τις γεωμετρικές ανισότητες , η παρακάτω δεν είναι πια πρωτότυπη...
Σκέφτομαι μήπως έχω κουράσει κάποιους με την έμφαση που έχω δώσει...
Σε τρίγωνοαποδείξτε ότι
Ζητώ συγνώμη γιατί αρχικά αντί γιαέγραψα




ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: Σε προηγούμενη δημοσίευση έδειξα ότι ανμήκη πλευρών τριγώνου , τότε οι
αποτελούν πλευρές τριγώνου με ακτίνα περιγεγραμμένου κύκλου ίση με
και με εμβαδόν το μισό του
Αν εφαρμόσουμε στο τρίγωνο με πλευρέςτην ανισότητα
προκύπτει ότι
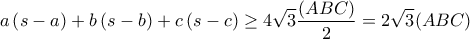
 ισούται με το εμβαδόν
ισούται με το εμβαδόν  .
.  έχουμε
έχουμε  και η ανισότητα γίνεται
και η ανισότητα γίνεται 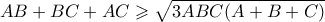 που είναι η ανισότητα Newton.
που είναι η ανισότητα Newton.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες