Αρχικά επειδή

, το παράκεντρο

ανήκει στον

Θεωρούμε τα σημεία

και

το σήμειο που εφάπτεται στον Παρεγγεγραμένο κύκλο η εφαπτομένη απο το

Θα δείξουμε πως

εφάπτεται και στον

στο

Πρώτον επειδή η πολική του

ως προς τον Παρεγγεγραμένο είναι η

και

, συμπεραίνουμε ( από Θεώρημα La Hire ) ότι

ανήκει στην πολική του

, δηλαδή

συνευθειακά
Τώρα θέλουμε να δείξουμε πως

είναι εγγράψιμο
Έστω

Θα είναι

και από τα Ορθογώνια τρίγωνα

και

συμπεραίνουμε πως

είναι μέσο της

Άρα

άρα,

εγγράψιμο, όπως θέλαμε.
Τέλος με δύναμη σημείου έχουμε

άρα
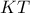
εφάπτεται στον

στο

, δηλαδή οι δύο κύκλοι έχουν κοινή εφαπτομένη στο

συνεπώς εφάπτονται στο


- mathematica geo.png (76.57 KiB) Προβλήθηκε 572 φορές
Νομίζω σχετικά γνωστή άσκηση
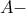 παρεγγεγραμμένος κύκλος οξυγώνιου τριγώνου
παρεγγεγραμμένος κύκλος οξυγώνιου τριγώνου  εφάπτεται στις πλευρές
εφάπτεται στις πλευρές 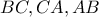 στα σημεία
στα σημεία  αντίστοιχα και η ευθεία
αντίστοιχα και η ευθεία  τέμνει τον περίκυκλο του τριγώνου
τέμνει τον περίκυκλο του τριγώνου  στα σημεία
στα σημεία  και
και  Αν
Αν  το μέσο του τμήματος
το μέσο του τμήματος  , να δείξετε ότι οι περίκυκλοι των τριγώνων
, να δείξετε ότι οι περίκυκλοι των τριγώνων  και
και  εφάπτονται.
εφάπτονται.
 , το παράκεντρο
, το παράκεντρο  ανήκει στον
ανήκει στον 
 και
και  το σήμειο που εφάπτεται στον Παρεγγεγραμένο κύκλο η εφαπτομένη απο το
το σήμειο που εφάπτεται στον Παρεγγεγραμένο κύκλο η εφαπτομένη απο το 
 εφάπτεται και στον
εφάπτεται και στον  στο
στο  ως προς τον Παρεγγεγραμένο είναι η
ως προς τον Παρεγγεγραμένο είναι η  και
και  , συμπεραίνουμε ( από Θεώρημα La Hire ) ότι
, συμπεραίνουμε ( από Θεώρημα La Hire ) ότι  , δηλαδή
, δηλαδή  συνευθειακά
συνευθειακά είναι εγγράψιμο
είναι εγγράψιμο
 και από τα Ορθογώνια τρίγωνα
και από τα Ορθογώνια τρίγωνα  και
και  συμπεραίνουμε πως
συμπεραίνουμε πως  είναι μέσο της
είναι μέσο της 

 άρα
άρα 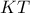 εφάπτεται στον
εφάπτεται στον  στο
στο  το
το  η δεύτερη τομή της ευθείας
η δεύτερη τομή της ευθείας  και
και  το μέσο του τμήματος
το μέσο του τμήματος 
 οπότε
οπότε  , όμως
, όμως 
 , τότε
, τότε  , οπότε
, οπότε  εγγράψιμο .
εγγράψιμο . και συνεπώς ο κύκλος
και συνεπώς ο κύκλος 
 , ο κύκλος
, ο κύκλος  γίνεται η ευθεία
γίνεται η ευθεία 
 , η οποία εφάπτεται του κύκλου
, η οποία εφάπτεται του κύκλου  Επομένως και στο αρχικό σχήμα, οι κύκλοι
Επομένως και στο αρχικό σχήμα, οι κύκλοι 