
Διοφαντική!!
Συντονιστές: cretanman, silouan, rek2
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Διοφαντική!!
Να βρεθούν όλες οι μη αρνητικές ακέραιες λύσεις της εξίσωσης 

Houston, we have a problem!
Λέξεις Κλειδιά:
Re: Διοφαντική!!
Λαθος απαντηση...
τελευταία επεξεργασία από thrassos σε Τρί Ιαν 10, 2017 10:10 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Θρασύβουλος Οικονόμου
Φοιτητής ΗΜΜΥ ΑΠΘ
Φοιτητής ΗΜΜΥ ΑΠΘ
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: Διοφαντική!!
Δεν είμαι τόσο σίγουρος για την αντιμετώπιση σουthrassos έγραψε:Καλησπέρα Διονύση,
Μια προσπάθεια για την άσκησή σου.
Αρχικά, γιαέχουμε ότι
με την ισότητα να ισχύει μόνο για
.Άρα μόνη λύση σε αυτή την περίπτωση η
.
Τώρα ακολουθώντας την ίδια τακτική για τηνέχουμε
.
Φιλικά,
Θράσος
 έχουμε και τη μη τετριμμένη λύση:
έχουμε και τη μη τετριμμένη λύση: και
και  .
. Φιλικά,
Διονύσης
Houston, we have a problem!
Re: Διοφαντική!!
Νομίζω το λαθος υπάρχει εκεί που το φράζεις ανάμεσα σε 2 τετράγωνα που όμως δεν ειναι τέλεια.Διονύσιος Αδαμόπουλος έγραψε:Δεν είμαι τόσο σίγουρος για την αντιμετώπιση σουthrassos έγραψε:Καλησπέρα Διονύση,
Μια προσπάθεια για την άσκησή σου.
Αρχικά, γιαέχουμε ότι
με την ισότητα να ισχύει μόνο για
.Άρα μόνη λύση σε αυτή την περίπτωση η
.
Τώρα ακολουθώντας την ίδια τακτική για τηνέχουμε
.
Φιλικά,
Θράσος. Για παράδειγμα στην
έχουμε και τη μη τετριμμένη λύση:
και
.
Φιλικά,
Διονύσης
Re: Διοφαντική!!
Διονύση νομίζω πως ειναι πολυ δύσκολη. Εσυ πώς την ελυσες;Διονύσιος Αδαμόπουλος έγραψε:Να βρεθούν όλες οι μη αρνητικές ακέραιες λύσεις της εξίσωσης
Re: Διοφαντική!!
Συμφωνώ. Νομίζω πάντως ότι υπάρχει ένας συσχετισμός με τηνΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Διονύση νομίζω πως ειναι πολυ δύσκολη. Εσυ πώς την ελυσες;Διονύσιος Αδαμόπουλος έγραψε:Να βρεθούν όλες οι μη αρνητικές ακέραιες λύσεις της εξίσωσης
 στον τρόπο λύσης της.
στον τρόπο λύσης της.EDIT: Λανθασμένη πληροφορία
τελευταία επεξεργασία από JimNt. σε Τρί Ιαν 10, 2017 9:40 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Bye :')
Re: Διοφαντική!!
Ποια είναι από ΒΜΟ;
Η άσκηση με είναι η άσκηση 2.71 από το βιβλίο Μαθηματικοί Διαγωνισμοί ΙΙ. Πρόκειται για αρκετά απαιτητική άσκηση.
είναι η άσκηση 2.71 από το βιβλίο Μαθηματικοί Διαγωνισμοί ΙΙ. Πρόκειται για αρκετά απαιτητική άσκηση.
Η άσκηση με
 είναι η άσκηση 2.71 από το βιβλίο Μαθηματικοί Διαγωνισμοί ΙΙ. Πρόκειται για αρκετά απαιτητική άσκηση.
είναι η άσκηση 2.71 από το βιβλίο Μαθηματικοί Διαγωνισμοί ΙΙ. Πρόκειται για αρκετά απαιτητική άσκηση.Σιλουανός Μπραζιτίκος
Re: Διοφαντική!!
Είχα δει κάτι παρεμφερές στο aops (silouan έγραψε:Ποια είναι από ΒΜΟ;
Η άσκηση μεείναι η άσκηση 2.71 από το βιβλίο Μαθηματικοί Διαγωνισμοί ΙΙ. Πρόκειται για αρκετά απαιτητική άσκηση.
 ,
,  ) και νόμισα ότι προέρχετο από BMO ,με συγχωρείτε.
) και νόμισα ότι προέρχετο από BMO ,με συγχωρείτε.Bye :')
-
panagiotis99
- Δημοσιεύσεις: 133
- Εγγραφή: Δευ Φεβ 04, 2013 8:24 pm
- Τοποθεσία: Αθηνα
Re: Διοφαντική!!
Ενώ ηΔιονύσιος Αδαμόπουλος έγραψε:Να βρεθούν όλες οι μη αρνητικές ακέραιες λύσεις της εξίσωσης
 πρόκειται για την εξίσωση του Ljunggren και η λύση της ξεφεύγει τελείως από την θεματική ενότητα.
πρόκειται για την εξίσωση του Ljunggren και η λύση της ξεφεύγει τελείως από την θεματική ενότητα.Καλό είναι πριν προτείνετε ασκήσεις να τις λύνεται πρώτα.
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: Διοφαντική!!
Καταρχάς, συγγνώμη αν σας ταλαιπώρησα χωρίς λόγο  . Κατασκεύασα αυτή την άσκηση στην προσπάθεια να δω αν υπάρχουν άπειροι αριθμοί
. Κατασκεύασα αυτή την άσκηση στην προσπάθεια να δω αν υπάρχουν άπειροι αριθμοί  που είναι τετράγωνοι(Οι λύσεις της εξίσωσης
που είναι τετράγωνοι(Οι λύσεις της εξίσωσης 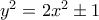 ) (Δεν γνώριζα πως ήταν εν μέρει άσκηση διαγωνισμού
) (Δεν γνώριζα πως ήταν εν μέρει άσκηση διαγωνισμού  ).
).
Για την πρώτη εξίσωση την δεν έχω κάποια πολύ περίπλοκη λύση (μπορεί να χάνω κάτι...)
δεν έχω κάποια πολύ περίπλοκη λύση (μπορεί να χάνω κάτι...)
Μια περιληπτική λύση:
Εύκολα μπορούμε να δείξουμε ότι το πρέπει να είναι άρτιος, άρα υποθέτουμε πως
πρέπει να είναι άρτιος, άρα υποθέτουμε πως  . Η εξίσωση γίνεται:
. Η εξίσωση γίνεται:

Οι αριθμοί και
και  είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι
είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι  και ότι
και ότι  ή
ή  και ότι
και ότι  . Η δεύτερη όμως περίπτωση απορρίπτεται, καθώς με αφαίρεση των δυο σχέσεων φτάνουμε σε άτοπο. Στη πρώτη περίπτωση αφαιρώντας τις δύο σχέσεις παίρνουμε ότι
. Η δεύτερη όμως περίπτωση απορρίπτεται, καθώς με αφαίρεση των δυο σχέσεων φτάνουμε σε άτοπο. Στη πρώτη περίπτωση αφαιρώντας τις δύο σχέσεις παίρνουμε ότι  . Οι αριθμοί
. Οι αριθμοί  και
και 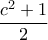 είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι
είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι  και ότι
και ότι  ή
ή  και ότι
και ότι  . Πάλι η δεύτερη περίπτωση απορρίπτεται, καθώς θα είχαμε ότι
. Πάλι η δεύτερη περίπτωση απορρίπτεται, καθώς θα είχαμε ότι 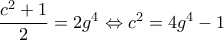 άτοπο. Άρα
άτοπο. Άρα  και
και  .
.
Προσθέτουμε τις δυο σχέσεις κατά μέλη και προκύπτει ότι . Αφαιρούμε τις δύο σχέσεις κατά μέλη και προκύπτει ότι
. Αφαιρούμε τις δύο σχέσεις κατά μέλη και προκύπτει ότι 
Αντικαθιστώντας την τελευταία στην πρώτη παίρνουμε ότι , άρα
, άρα  και επιστρέφοντας στην αρχική παίρνουμε την μοναδική λύση
και επιστρέφοντας στην αρχική παίρνουμε την μοναδική λύση  και
και  .
.
Για την βρήκα ένα μικρό λάθος που μου καταστρέφει το σκεπτικό
βρήκα ένα μικρό λάθος που μου καταστρέφει το σκεπτικό  . Πραγματικά δεν έχω λύση. Πάντως εκτός από την τετριμμένη
. Πραγματικά δεν έχω λύση. Πάντως εκτός από την τετριμμένη  , υπάρχει και η
, υπάρχει και η  και μπορεί και περισσότερες...
και μπορεί και περισσότερες...
 που είναι τετράγωνοι(Οι λύσεις της εξίσωσης
που είναι τετράγωνοι(Οι λύσεις της εξίσωσης 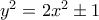 ) (Δεν γνώριζα πως ήταν εν μέρει άσκηση διαγωνισμού
) (Δεν γνώριζα πως ήταν εν μέρει άσκηση διαγωνισμού Για την πρώτη εξίσωση την
 δεν έχω κάποια πολύ περίπλοκη λύση (μπορεί να χάνω κάτι...)
δεν έχω κάποια πολύ περίπλοκη λύση (μπορεί να χάνω κάτι...)Μια περιληπτική λύση:
Εύκολα μπορούμε να δείξουμε ότι το
 πρέπει να είναι άρτιος, άρα υποθέτουμε πως
πρέπει να είναι άρτιος, άρα υποθέτουμε πως  . Η εξίσωση γίνεται:
. Η εξίσωση γίνεται:
Οι αριθμοί
 και
και  είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι
είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι  και ότι
και ότι  ή
ή  και ότι
και ότι  . Η δεύτερη όμως περίπτωση απορρίπτεται, καθώς με αφαίρεση των δυο σχέσεων φτάνουμε σε άτοπο. Στη πρώτη περίπτωση αφαιρώντας τις δύο σχέσεις παίρνουμε ότι
. Η δεύτερη όμως περίπτωση απορρίπτεται, καθώς με αφαίρεση των δυο σχέσεων φτάνουμε σε άτοπο. Στη πρώτη περίπτωση αφαιρώντας τις δύο σχέσεις παίρνουμε ότι  . Οι αριθμοί
. Οι αριθμοί  και
και 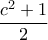 είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι
είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι  και ότι
και ότι  ή
ή  και ότι
και ότι  . Πάλι η δεύτερη περίπτωση απορρίπτεται, καθώς θα είχαμε ότι
. Πάλι η δεύτερη περίπτωση απορρίπτεται, καθώς θα είχαμε ότι 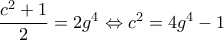 άτοπο. Άρα
άτοπο. Άρα  και
και  .
.Προσθέτουμε τις δυο σχέσεις κατά μέλη και προκύπτει ότι
 . Αφαιρούμε τις δύο σχέσεις κατά μέλη και προκύπτει ότι
. Αφαιρούμε τις δύο σχέσεις κατά μέλη και προκύπτει ότι 
Αντικαθιστώντας την τελευταία στην πρώτη παίρνουμε ότι
 , άρα
, άρα  και επιστρέφοντας στην αρχική παίρνουμε την μοναδική λύση
και επιστρέφοντας στην αρχική παίρνουμε την μοναδική λύση  και
και  .
.Για την
 βρήκα ένα μικρό λάθος που μου καταστρέφει το σκεπτικό
βρήκα ένα μικρό λάθος που μου καταστρέφει το σκεπτικό  , υπάρχει και η
, υπάρχει και η  και μπορεί και περισσότερες...
και μπορεί και περισσότερες...Houston, we have a problem!
Re: Διοφαντική!!
Μονο αυτές οι δυο ειναι.Διονύσιος Αδαμόπουλος έγραψε:Καταρχάς, συγγνώμη αν σας ταλαιπώρησα χωρίς λόγο. Κατασκεύασα αυτή την άσκηση στην προσπάθεια να δω αν υπάρχουν άπειροι αριθμοί
που είναι τετράγωνοι(Οι λύσεις της εξίσωσης
) (Δεν γνώριζα πως ήταν εν μέρει άσκηση διαγωνισμού
).
Για την πρώτη εξίσωση τηνδεν έχω κάποια πολύ περίπλοκη λύση (μπορεί να χάνω κάτι...)
Μια περιληπτική λύση:
Εύκολα μπορούμε να δείξουμε ότι τοπρέπει να είναι άρτιος, άρα υποθέτουμε πως
. Η εξίσωση γίνεται:
Οι αριθμοίκαι
είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι
και ότι
ή
και ότι
. Η δεύτερη όμως περίπτωση απορρίπτεται, καθώς με αφαίρεση των δυο σχέσεων φτάνουμε σε άτοπο. Στη πρώτη περίπτωση αφαιρώντας τις δύο σχέσεις παίρνουμε ότι
. Οι αριθμοί
και
είναι πρώτοι μεταξύ τους, άρα αναγκαστικά παίρνουμε ότι
και ότι
ή
και ότι
. Πάλι η δεύτερη περίπτωση απορρίπτεται, καθώς θα είχαμε ότι
άτοπο. Άρα
και
.
Προσθέτουμε τις δυο σχέσεις κατά μέλη και προκύπτει ότι. Αφαιρούμε τις δύο σχέσεις κατά μέλη και προκύπτει ότι
Αντικαθιστώντας την τελευταία στην πρώτη παίρνουμε ότι, άρα
και επιστρέφοντας στην αρχική παίρνουμε την μοναδική λύση
και
.
Για τηνβρήκα ένα μικρό λάθος που μου καταστρέφει το σκεπτικό
. Πραγματικά δεν έχω λύση. Πάντως εκτός από την τετριμμένη
, υπάρχει και η
και μπορεί και περισσότερες...
Καλο βράδυ.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Διοφαντική!!
Βρήκα μια λύση αρκετά μακροσκελή μεν, αλλά που βασίζεται μόνο σε γνώσεις ολυμπιάδων. (Μεταφέρω λοιπόν το θέμα στο Προχωρημένο Επίπεδο των Seniors.)
Η λύση ακολουθεί το μοτίβο της απόδειξης ότι το μόνα τέλεια τετράγωνα στην ακολουθία Fibonacci είναι το και το
και το  .
.
Σκιαγραφώ τα σημεία της απόδειξης χωρίς όμως να βάζω πλήρεις λεπτομέρειες.
Ξεκινάμε από τις εξισώσεις Pell . Από την θεωρία της εξίσωσης Pell οι θετικές λύσεις είναι της μορφής
. Από την θεωρία της εξίσωσης Pell οι θετικές λύσεις είναι της μορφής  . Η ακολουθία
. Η ακολουθία  ορίζεται από τις αρχικές τιμές
ορίζεται από τις αρχικές τιμές  και τον αναδρομικό τύπο
και τον αναδρομικό τύπο  . Η ακολουθία
. Η ακολουθία  ορίζεται από τις αρχικές τιμές
ορίζεται από τις αρχικές τιμές  και τον αναδρομικό τύπο
και τον αναδρομικό τύπο  .
.
Οι πρώτοι όροι της είναι οι
είναι οι  .
.
Οι πρώτοι όροι της είναι οι
είναι οι  .
.
Θέλουμε να δείξουμε ότι τα μόνα τέλεια τετράγωνα της ακολουθίας είναι τα
είναι τα  και
και  . Οπότε και οι μοναδικές λύσεις της διοφαντικής θα είναι οι
. Οπότε και οι μοναδικές λύσεις της διοφαντικής θα είναι οι  και
και  .
.
Mod 4, η ακολουθία γίνεται
γίνεται  και μετά επαναλαμβάνεται. Οπότε για
και μετά επαναλαμβάνεται. Οπότε για  ο
ο  δεν είναι τέλειο τετράγωνο.
δεν είναι τέλειο τετράγωνο.
Mod 3, η ακολουθία γίνεται
γίνεται  και μετά επαναλαμβάνεται. Οπότε για
και μετά επαναλαμβάνεται. Οπότε για  ο
ο  δεν είναι τέλειο τετράγωνο.
δεν είναι τέλειο τετράγωνο.
Μένει να ελέγξουμε τις περιπτώσεις .
.
Θέτω . Πάλι από γνωστή θεωρία μπορεί να δειχθεί ότι
. Πάλι από γνωστή θεωρία μπορεί να δειχθεί ότι
 και
και 
[Από την στιγμή βέβαια που τα βρήκαμε, ελέγχονται εύκολα επαγωγικά.]
Χρησιμοποιώντας αυτούς τους τύπους μπορώ να δείξω με απλή άλγεβρα ότι
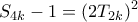 και
και 
Μπορώ επίσης να δείξω ότι

Το τελευταίο δίνει και επειδή
και επειδή  (είναι λύσεις της Pell) με τον
(είναι λύσεις της Pell) με τον  να είναι περιττός πρέπει ο
να είναι περιττός πρέπει ο  να είναι τέλειο τετράγωνο. Όμως δείξαμε πιο πάνω ότι ο
να είναι τέλειο τετράγωνο. Όμως δείξαμε πιο πάνω ότι ο  διαφέρει ακριβώς κατά
διαφέρει ακριβώς κατά  από ένα τέλειο τετράγωνο. Αυτό είναι άτοπο. (Εκτός για το
από ένα τέλειο τετράγωνο. Αυτό είναι άτοπο. (Εκτός για το  που δεν το λαμβάνουμε υπόψη επειδή τότε
που δεν το λαμβάνουμε υπόψη επειδή τότε  που δεν είναι θετικό.)
που δεν είναι θετικό.)
Άρα απορρίψαμε και τα και μένουν τα
και μένουν τα  .
.
Ας υποθέσουμε ότι . O
. O  δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι
δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι  . Μπορούμε να γράψουμε
. Μπορούμε να γράψουμε  με
με  . (Επιτρέπεται
. (Επιτρέπεται  .)
.)
Χρησιμοποιώντας επαναλαμβανόμενα την με
με  καταλήγουμε στο
καταλήγουμε στο

Όμως και άρα διαιρείται με έναν πρώτο
και άρα διαιρείται με έναν πρώτο  της μορφής
της μορφής  . Επειδή όμως το
. Επειδή όμως το  δεν είναι τέλειο τετράγωνο
δεν είναι τέλειο τετράγωνο 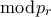 , δεν υπάρχουν ούτε άλλες λύσεις της μορφής
, δεν υπάρχουν ούτε άλλες λύσεις της μορφής  εκτός από την
εκτός από την  .
.
Μένει η περίπτωση . O
. O  δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι
δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι  . Ακολουθούμε ακριβώς την ίδια τακτική. Μπορούμε να γράψουμε
. Ακολουθούμε ακριβώς την ίδια τακτική. Μπορούμε να γράψουμε  με
με  . Παίρνουμε
. Παίρνουμε

Όμως ούτε το είναι τέλειο τετράγωνο
είναι τέλειο τετράγωνο 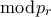 οπότε για
οπότε για  η μοναδική λύση είναι η
η μοναδική λύση είναι η  .
.
Η απόδειξη ολοκληρώθηκε.
Η λύση ακολουθεί το μοτίβο της απόδειξης ότι το μόνα τέλεια τετράγωνα στην ακολουθία Fibonacci είναι το
 και το
και το  .
.Σκιαγραφώ τα σημεία της απόδειξης χωρίς όμως να βάζω πλήρεις λεπτομέρειες.
Ξεκινάμε από τις εξισώσεις Pell
 . Από την θεωρία της εξίσωσης Pell οι θετικές λύσεις είναι της μορφής
. Από την θεωρία της εξίσωσης Pell οι θετικές λύσεις είναι της μορφής  . Η ακολουθία
. Η ακολουθία  ορίζεται από τις αρχικές τιμές
ορίζεται από τις αρχικές τιμές  και τον αναδρομικό τύπο
και τον αναδρομικό τύπο  . Η ακολουθία
. Η ακολουθία  ορίζεται από τις αρχικές τιμές
ορίζεται από τις αρχικές τιμές  και τον αναδρομικό τύπο
και τον αναδρομικό τύπο  .
.Οι πρώτοι όροι της
 είναι οι
είναι οι  .
.Οι πρώτοι όροι της
 είναι οι
είναι οι  .
.Θέλουμε να δείξουμε ότι τα μόνα τέλεια τετράγωνα της ακολουθίας
 είναι τα
είναι τα  και
και  . Οπότε και οι μοναδικές λύσεις της διοφαντικής θα είναι οι
. Οπότε και οι μοναδικές λύσεις της διοφαντικής θα είναι οι  και
και  .
.Mod 4, η ακολουθία
 γίνεται
γίνεται  και μετά επαναλαμβάνεται. Οπότε για
και μετά επαναλαμβάνεται. Οπότε για  ο
ο  δεν είναι τέλειο τετράγωνο.
δεν είναι τέλειο τετράγωνο. Mod 3, η ακολουθία
 γίνεται
γίνεται  και μετά επαναλαμβάνεται. Οπότε για
και μετά επαναλαμβάνεται. Οπότε για  ο
ο  δεν είναι τέλειο τετράγωνο.
δεν είναι τέλειο τετράγωνο.Μένει να ελέγξουμε τις περιπτώσεις
 .
.Θέτω
 . Πάλι από γνωστή θεωρία μπορεί να δειχθεί ότι
. Πάλι από γνωστή θεωρία μπορεί να δειχθεί ότι  και
και 
[Από την στιγμή βέβαια που τα βρήκαμε, ελέγχονται εύκολα επαγωγικά.]
Χρησιμοποιώντας αυτούς τους τύπους μπορώ να δείξω με απλή άλγεβρα ότι
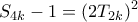 και
και 
Μπορώ επίσης να δείξω ότι

Το τελευταίο δίνει
 και επειδή
και επειδή  (είναι λύσεις της Pell) με τον
(είναι λύσεις της Pell) με τον  να είναι περιττός πρέπει ο
να είναι περιττός πρέπει ο  να είναι τέλειο τετράγωνο. Όμως δείξαμε πιο πάνω ότι ο
να είναι τέλειο τετράγωνο. Όμως δείξαμε πιο πάνω ότι ο  διαφέρει ακριβώς κατά
διαφέρει ακριβώς κατά  από ένα τέλειο τετράγωνο. Αυτό είναι άτοπο. (Εκτός για το
από ένα τέλειο τετράγωνο. Αυτό είναι άτοπο. (Εκτός για το  που δεν το λαμβάνουμε υπόψη επειδή τότε
που δεν το λαμβάνουμε υπόψη επειδή τότε  που δεν είναι θετικό.)
που δεν είναι θετικό.)Άρα απορρίψαμε και τα
 και μένουν τα
και μένουν τα  .
.Ας υποθέσουμε ότι
 . O
. O  δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι
δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι  . Μπορούμε να γράψουμε
. Μπορούμε να γράψουμε  με
με  . (Επιτρέπεται
. (Επιτρέπεται  .)
.)Χρησιμοποιώντας επαναλαμβανόμενα την
 με
με  καταλήγουμε στο
καταλήγουμε στο 
Όμως
 και άρα διαιρείται με έναν πρώτο
και άρα διαιρείται με έναν πρώτο  της μορφής
της μορφής  . Επειδή όμως το
. Επειδή όμως το  δεν είναι τέλειο τετράγωνο
δεν είναι τέλειο τετράγωνο 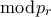 , δεν υπάρχουν ούτε άλλες λύσεις της μορφής
, δεν υπάρχουν ούτε άλλες λύσεις της μορφής  εκτός από την
εκτός από την  .
.Μένει η περίπτωση
 . O
. O  δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι
δίνει τέλειο τετράγωνο οπότε ας υποθέσουμε ότι  . Ακολουθούμε ακριβώς την ίδια τακτική. Μπορούμε να γράψουμε
. Ακολουθούμε ακριβώς την ίδια τακτική. Μπορούμε να γράψουμε  με
με  . Παίρνουμε
. Παίρνουμε
Όμως ούτε το
 είναι τέλειο τετράγωνο
είναι τέλειο τετράγωνο 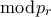 οπότε για
οπότε για  η μοναδική λύση είναι η
η μοναδική λύση είναι η  .
.Η απόδειξη ολοκληρώθηκε.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
