 που ικανοποιούν την:
που ικανοποιούν την:
Συντονιστές: cretanman, silouan, rek2
 που ικανοποιούν την:
που ικανοποιούν την:
Επαναφορά!ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Βρείτε όλα τα ζεύγη θετικών ακεραίωνπου ικανοποιούν την:
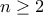 .
. οι πρώτοι διαιρέτες του αριθμού
οι πρώτοι διαιρέτες του αριθμού  .
. τότε
τότε  και
και  οπότε από τη δοσμένη σχέση προκύπτει ότι
οπότε από τη δοσμένη σχέση προκύπτει ότι  Ειδικότερα, ο
Ειδικότερα, ο  είναι περιττός, οπότε από το μικρό θεώρημα του Fermat έχουμε ότι
είναι περιττός, οπότε από το μικρό θεώρημα του Fermat έχουμε ότι  Επομένως, αν
Επομένως, αν  τότε
τότε  και αν πάρουμε έναν πρώτο διαιρέτη
και αν πάρουμε έναν πρώτο διαιρέτη  του
του  , τότε θα έχουμε ότι
, τότε θα έχουμε ότι  και
και  πράγμα άτοπο.
πράγμα άτοπο.
![\displaystyle{n - \varphi \left( n \right) - 1 = n\left[ {1 - \prod\limits_{i = 1}^k {\left( {1 - \frac{1}{{{p_i}}}} \right)} } \right] - 1.} \displaystyle{n - \varphi \left( n \right) - 1 = n\left[ {1 - \prod\limits_{i = 1}^k {\left( {1 - \frac{1}{{{p_i}}}} \right)} } \right] - 1.}](/forum/ext/geomar/texintegr/latexrender/pictures/2371b3bbd71fc68fd7635c608504b5ca.png)
 για κάθε
για κάθε  έχουμε ότι:
έχουμε ότι:

 .
.



 προκύπτει ότι αν
προκύπτει ότι αν  ή
ή  τότε
τότε  και από τα παραπάνω καταλήγουμε σε άτοπο.
και από τα παραπάνω καταλήγουμε σε άτοπο. και
και  δηλαδή
δηλαδή  ή
ή 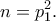
 Αν
Αν  τότε η δοσμένη σχέση γράφεται ισοδύναμα
τότε η δοσμένη σχέση γράφεται ισοδύναμα  οπότε
οπότε 
 Αν
Αν  τότε η δοσμένη σχέση γράφεται ισοδύναμα
τότε η δοσμένη σχέση γράφεται ισοδύναμα 
 .
. τότε η σχέση
τότε η σχέση  δίνει ότι
δίνει ότι  και
και  .
. είναι περιττός, τότε
είναι περιττός, τότε  οπότε η σχέση
οπότε η σχέση  δίνει ότι
δίνει ότι  Αλλά για
Αλλά για  είναι
είναι  οπότε πρέπει
οπότε πρέπει  Τότε, η σχέση
Τότε, η σχέση  δίνει ότι
δίνει ότι  που είναι άτοπο.
που είναι άτοπο. .
.Σας ευχαριστώ πολύ για τις όμορφες και περιποιημένες λύσεις που δίνετε!emouroukos έγραψε:Πρώτα απ' όλα, παρατηρούμε ότι πρέπει.
Έστωοι πρώτοι διαιρέτες του αριθμού
.
Αν υποθέσουμε ότιτότε
και
οπότε από τη δοσμένη σχέση προκύπτει ότι
Ειδικότερα, ο
είναι περιττός, οπότε από το μικρό θεώρημα του Fermat έχουμε ότι
Επομένως, αν
τότε
και αν πάρουμε έναν πρώτο διαιρέτη
του
, τότε θα έχουμε ότι
και
πράγμα άτοπο.
Είναι γνωστό ότι

οπότε
Επειδήγια κάθε
έχουμε ότι:
οπότε

.
Παρατηρούμε τώρα ότι:


Συνεπώς, από τη σχέσηπροκύπτει ότι αν
ή
τότε
και από τα παραπάνω καταλήγουμε σε άτοπο.
Έτσι, πρέπεικαι
δηλαδή
ή
Αν
τότε η δοσμένη σχέση γράφεται ισοδύναμα
οπότε
Αν
τότε η δοσμένη σχέση γράφεται ισοδύναμα

.
Αντότε η σχέση
δίνει ότι
και
.
Αν οείναι περιττός, τότε
οπότε η σχέση
δίνει ότι
Αλλά για
είναι
οπότε πρέπει
Τότε, η σχέση
δίνει ότι
που είναι άτοπο.
Ώστε, η δοσμένη εξίσωση έχει τις λύσεις.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες