 ,
, 
Συντονιστής: stranton

 Έχω
Έχω  .
.
 Έχω
Έχω  με
με 
 η (1) ισχύει για κάθε
η (1) ισχύει για κάθε 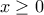 .
. η (1) γίνεται
η (1) γίνεται  που ισχύει για κάθε
που ισχύει για κάθε 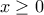 .
. έχουμε
έχουμε  για
για  και η (1) ισχύει για κάθε
και η (1) ισχύει για κάθε 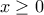 .
. Έχω
Έχω  με
με 
 η (1) ισχύει για κάθε
η (1) ισχύει για κάθε  .
. η (1) γίνεται
η (1) γίνεται  που ισχύει για κάθε
που ισχύει για κάθε  .
. έχουμε
έχουμε  για
για  και η (1) ισχύει για κάθε
και η (1) ισχύει για κάθε  .
.
 Έχω
Έχω  με
με 
 η (1) είναι αδύνατη.
η (1) είναι αδύνατη. η (1) γίνεται
η (1) γίνεται  (αδύνατη).
(αδύνατη). έχουμε
έχουμε  για
για  και η (1) ισχύει για κάθε
και η (1) ισχύει για κάθε  .
. Έχω
Έχω  με
με 
 η (1) είναι αδύνατη.
η (1) είναι αδύνατη. η (1) γίνεται
η (1) γίνεται  (αδύνατη).
(αδύνατη). έχουμε
έχουμε  για
για  και η (1) ισχύει για κάθε
και η (1) ισχύει για κάθε  .
.Χμμμ. Στην παραπάνω λύση χανόμαστε στις περιπτώσεις και δεν βλέπουμε τι γίνεται (άσε που νομίζω - μπορεί να κάνω λάθος- ότι η λύση είναι ελλειπής).KARKAR έγραψε:Έχετε υπομονή ; Αν ναι , τότε λύστε την ανίσωση :,
 τότε η ανίσωση γίνεται
τότε η ανίσωση γίνεται  , που είναι άμεση (συγκεκριμένα,
, που είναι άμεση (συγκεκριμένα,  ).
). . Τότε είναι προφανές ότι το αριστερό μέλος είναι γνήσια θετικό (άθροισμα θετικών) οπότε η ανίσωση επαληθεύεται για κάθε
. Τότε είναι προφανές ότι το αριστερό μέλος είναι γνήσια θετικό (άθροισμα θετικών) οπότε η ανίσωση επαληθεύεται για κάθε 
 , διαιρούμε με το
, διαιρούμε με το  και η ανίσωση γράφεται
και η ανίσωση γράφεται  . Θα μας χρειαστεί η διακρίνουσα, η οποία είναι
. Θα μας χρειαστεί η διακρίνουσα, η οποία είναι  . Παρατηρούμε ότι οι όροι
. Παρατηρούμε ότι οι όροι 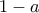 και
και  είναι θετικοί ούτως ή άλλως. Άρα η δαικρίνουσα είναι π.χ.
είναι θετικοί ούτως ή άλλως. Άρα η δαικρίνουσα είναι π.χ.  αν και μόνον αν
αν και μόνον αν  , που σημαίνει
, που σημαίνει  . Στη περίπτωση αυτή, επειδή ο συντελεστής του
. Στη περίπτωση αυτή, επειδή ο συντελεστής του  είναι θετικός, το τριώνυμο είναι
είναι θετικός, το τριώνυμο είναι  , δηλαδή δεν υπάρχουν λύσεις.
, δηλαδή δεν υπάρχουν λύσεις.  . H λύση είναι για
. H λύση είναι για  μεταξύ των ριζών. Αφήνω τις λεπτομέρειες απλά σημειώνω ότι γλυτώνουμε κόπο αν παρατηρήσουμε ότι οι ρίζες του τριωνύμου είναι ομόσημες (γινόμενο = 1), οπότε μας ενδιαφέρει πότε το άθροισμά τους είναι θετικό ή μη. Αυτό είναι απλό γιατί ανάγεται στο
μεταξύ των ριζών. Αφήνω τις λεπτομέρειες απλά σημειώνω ότι γλυτώνουμε κόπο αν παρατηρήσουμε ότι οι ρίζες του τριωνύμου είναι ομόσημες (γινόμενο = 1), οπότε μας ενδιαφέρει πότε το άθροισμά τους είναι θετικό ή μη. Αυτό είναι απλό γιατί ανάγεται στο  , αλλά αφού
, αλλά αφού  , ισοδυναμεί με
, ισοδυναμεί με  . Και λοιπά.
. Και λοιπά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες