 ) εξίσωση :
) εξίσωση :  ,η οποία έχει ακριβώς μία λύση διαφορετική από τους αριθμούς
,η οποία έχει ακριβώς μία λύση διαφορετική από τους αριθμούς  και
και  ,
,ενώ για τον αριθμό
 είναι γνωστό ότι
είναι γνωστό ότι 
![A=\left [ -1,-\frac{1}{2} \right ]\cup \left [\frac{1}{2},1 \right ]\cup \left [ 2, \frac{5}{2}\right ] A=\left [ -1,-\frac{1}{2} \right ]\cup \left [\frac{1}{2},1 \right ]\cup \left [ 2, \frac{5}{2}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/8590255f9a70b6947041b5e1ea2d8c4c.png) .
. Να βρεθούν οι ρίζες της εξίσωσης .
Συντονιστής: stranton
 ) εξίσωση :
) εξίσωση :  ,η οποία έχει ακριβώς μία λύση διαφορετική από τους αριθμούς
,η οποία έχει ακριβώς μία λύση διαφορετική από τους αριθμούς  και
και  ,
, είναι γνωστό ότι
είναι γνωστό ότι 
![A=\left [ -1,-\frac{1}{2} \right ]\cup \left [\frac{1}{2},1 \right ]\cup \left [ 2, \frac{5}{2}\right ] A=\left [ -1,-\frac{1}{2} \right ]\cup \left [\frac{1}{2},1 \right ]\cup \left [ 2, \frac{5}{2}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/8590255f9a70b6947041b5e1ea2d8c4c.png) .
. Χαιρετώ τον Μιχάλη και κάνω μια προσπάθεια. Επειδή βρέθηκα σε χωράφια ξένα της Α΄ Λυκείου φοβάμαι μήπως έχω κάποιο λάθος.maiksoul έγραψε:Έστω η (με άγνωστο τον) εξίσωση :
,η οποία έχει ακριβώς μία λύση διαφορετική από τους αριθμούς
και
,
ενώ για τον αριθμόείναι γνωστό ότι

.
Να βρεθούν οι ρίζες της εξίσωσης .
 έχει διακρίνουσα
έχει διακρίνουσα 
 (2)
(2) η (2) γίνεται
η (2) γίνεται  .
. , που απορρίπτεται αφού δεν ανήκει στο
, που απορρίπτεται αφού δεν ανήκει στο  .
.  ) γίνεται
) γίνεται  .
. με
με  .
.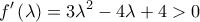 για κάθε
για κάθε  άρα η συνάρτηση
άρα η συνάρτηση  είναι γνησίως αύξουσα. Είναι
είναι γνησίως αύξουσα. Είναι  και
και  , άρα, αφού είναι συνεχής στο
, άρα, αφού είναι συνεχής στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) , από Θ. Bolzano, έχει μια ρίζα στο
, από Θ. Bolzano, έχει μια ρίζα στο 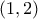 , που δεν ανήκει στο
, που δεν ανήκει στο  , άρα η αρχική εξίσωση δεν μπορεί να έχει διπλή ρίζα.
, άρα η αρχική εξίσωση δεν μπορεί να έχει διπλή ρίζα.Καλησπέρα σε όλους!maiksoul έγραψε:Έστω η (με άγνωστο τον) εξίσωση :
,η οποία έχει ακριβώς μία λύση διαφορετική από τους αριθμούς
και
,
ενώ για τον αριθμόείναι γνωστό ότι

.
Να βρεθούν οι ρίζες της εξίσωσης .
 είναι η μονάδα. Η μόνη περίπτωση λοιπόν, είναι η εξίσωση να έχει δύο ρίζες εκ των οποίων η μία να είναι
είναι η μονάδα. Η μόνη περίπτωση λοιπόν, είναι η εξίσωση να έχει δύο ρίζες εκ των οποίων η μία να είναι  ή
ή  που απορρίπτονται.
που απορρίπτονται. 

 η διακρίνουσα
η διακρίνουσα  είναι θετική μόνο στο
είναι θετική μόνο στο ![\displaystyle{\left[ {2,\frac{5}{2}} \right]} \displaystyle{\left[ {2,\frac{5}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/a56f20b5960d94d0abdf1e52e83a29e0.png)
 η εξίσωση γράφεται
η εξίσωση γράφεται  που είναι άτοπο αφού
που είναι άτοπο αφού ![\displaystyle{\lambda \in \left[ {2,\frac{5}{2}} \right]} \displaystyle{\lambda \in \left[ {2,\frac{5}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/8708388b4c3d358f45e906d6e8585972.png)
 τότε προκύπτει ότι
τότε προκύπτει ότι  και εύκολα βρίσκουμε ότι
και εύκολα βρίσκουμε ότι 
Πάντως, θα χαρώ να δω τόσο την επίλυση της εξίσωσης (2) όσο και το πρόσημο της Διακρίνουσας λυμένα με εργαλεία της Α΄ Λυκείου.george visvikis έγραψε: Από τα διαστήματα που δίνονται για τοη διακρίνουσα
είναι θετική μόνο στο
![\displaystyle{\left[ {2,\frac{5}{2}} \right]} \displaystyle{\left[ {2,\frac{5}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/a56f20b5960d94d0abdf1e52e83a29e0.png)
Καλημέρα Γιώργο, καλημέρα σε όλους!Γιώργος Ρίζος έγραψε:Πάντως, θα χαρώ να δω τόσο την επίλυση της εξίσωσης (2) όσο και το πρόσημο της Διακρίνουσας λυμένα με εργαλεία της Α΄ Λυκείου.george visvikis έγραψε: Από τα διαστήματα που δίνονται για τοη διακρίνουσα
είναι θετική μόνο στο
![\displaystyle{\left[ {2,\frac{5}{2}} \right]} \displaystyle{\left[ {2,\frac{5}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/a56f20b5960d94d0abdf1e52e83a29e0.png)
 χρησιμοποιώντας Horner και
χρησιμοποιώντας Horner και  εξέτασα το πρόσημο του
εξέτασα το πρόσημο του  στα διαστήματα που έδινε. Προηγουμένως όμως είχα
στα διαστήματα που έδινε. Προηγουμένως όμως είχα 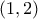 (με τρόπο εκτός ύλης).
(με τρόπο εκτός ύλης). είναι
είναι 

 η τελευταία δεν έχει αρνητική ρίζα, επομένως αν έχει θα έχει κάποια από το Α, θετική.Εδώ τώρα έχει το δικό της ενδιαφέρον να δειχθεί ότι η τελευταία δεν έχει ούτε κάποια θετική ρίζα από το Α.Το αφήνω προς το παρόν για να ασχοληθούν και κάποιοι άλλοι, αν το επιθυμούν.
η τελευταία δεν έχει αρνητική ρίζα, επομένως αν έχει θα έχει κάποια από το Α, θετική.Εδώ τώρα έχει το δικό της ενδιαφέρον να δειχθεί ότι η τελευταία δεν έχει ούτε κάποια θετική ρίζα από το Α.Το αφήνω προς το παρόν για να ασχοληθούν και κάποιοι άλλοι, αν το επιθυμούν.Καλημέρα Μιχάλη!maiksoul έγραψε:Γιώργο και Γιώργο Καλημέρα,μια λύση για τηνείναι
η τελευταία δεν έχει αρνητική ρίζα, επομένως αν έχει θα έχει κάποια από το Α, θετική.Εδώ τώρα έχει το δικό της ενδιαφέρον να δειχθεί ότι η τελευταία δεν έχει ούτε κάποια θετική ρίζα από το Α.Το αφήνω προς το παρόν για να ασχοληθούν και κάποιοι άλλοι, αν το επιθυμούν.
 έχει μία θετική ρίζα.
έχει μία θετική ρίζα. γιατί
γιατί 
 γιατί
γιατί 
 , που είναι άτοπο. Άρα η εξίσωση δεν έχει ρίζα στο
, που είναι άτοπο. Άρα η εξίσωση δεν έχει ρίζα στο 
Καλημέρα Γιώργο , ναι αυτή είναι μια από τις λύσεις!george visvikis έγραψε:Καλημέρα Μιχάλη!maiksoul έγραψε:Γιώργο και Γιώργο Καλημέρα,μια λύση για τηνείναι
η τελευταία δεν έχει αρνητική ρίζα, επομένως αν έχει θα έχει κάποια από το Α, θετική.Εδώ τώρα έχει το δικό της ενδιαφέρον να δειχθεί ότι η τελευταία δεν έχει ούτε κάποια θετική ρίζα από το Α.Το αφήνω προς το παρόν για να ασχοληθούν και κάποιοι άλλοι, αν το επιθυμούν.
Έστω ότι η εξίσωσηέχει μία θετική ρίζα.
Δεν μπορεί όμως να είναιγιατί
Δεν μπορεί να είναι ούτεγιατί
, που είναι άτοπο. Άρα η εξίσωση δεν έχει ρίζα στο
Με ύλη Α΄Λυκείου.maiksoul έγραψε:Έστω η (με άγνωστο τον) εξίσωση :
,η οποία έχει ακριβώς μία λύση διαφορετική από τους αριθμούς
και
,
ενώ για τον αριθμόείναι γνωστό ότι

.
Να βρεθούν οι ρίζες της εξίσωσης .
 οι ρίζες της δευτεροβάθμιας εξίσωσης, είναι:
οι ρίζες της δευτεροβάθμιας εξίσωσης, είναι:  και
και  .
. 
![A=\left [ -1,-\frac{1}{2} \right ]\cup \left [\frac{1}{2},1 \right ]\cup \left [ 2, \frac{5}{2}\right ] A=\left [ -1,-\frac{1}{2} \right ]\cup \left [\frac{1}{2},1 \right ]\cup \left [ 2, \frac{5}{2}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/8590255f9a70b6947041b5e1ea2d8c4c.png) άρα
άρα  .
. έχουν αρνητικό άθροισμα και θετικό γινόμενο θα είναι και οι δύο αρνητικές,
έχουν αρνητικό άθροισμα και θετικό γινόμενο θα είναι και οι δύο αρνητικές,  και έτσι,
και έτσι, 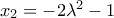 .
.  ή
ή 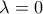 .
.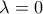 απορρίπτεται λόγω περιορισμών ενώ η τιμή
απορρίπτεται λόγω περιορισμών ενώ η τιμή  είναι δεκτή
είναι δεκτή  .
. και
και  .
. παρουσιάζει ελάχιστο στο
παρουσιάζει ελάχιστο στο  το
το  .
. και άρα η εξίσωση :
και άρα η εξίσωση :  είναι αδύνατη
είναι αδύνατη![\Delta = [2,\dfrac{5}{2}] \Delta = [2,\dfrac{5}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/95d7e2aeac9823121b985eab2d683413.png) ,
,  συνεπώς η εξίσωση
συνεπώς η εξίσωση  έχει δύο
έχει δύο  και η πιο μικρή
και η πιο μικρή  με το ίσον να πιάνεται αν
με το ίσον να πιάνεται αν  .
.Καλό απόγευμα Μιχάλη,maiksoul έγραψε:Καλημέρα nikkru (Νίκο;...)! Σε ευχαριστώ για τον χρόνο σου.Στην απάντηση σου έχω να παρατηρήσω τα εξής:
1) Στην λύση σου θεωρείς ότι οι (αρνητικές..όπως πολύ σωστά επισημαίνεις..) ρίζες τις εξίσωσης , είναι...διαφορετικές μεταξύ τους.Αυτό όμως δεν είναι το μοναδικό που μπορεί να συμβεί και ούτε προκύπτει αναγκαστικά από τα δεδομένα.
2)Πρέπει να συμπληρωθεί η λύση σου , με το τι γίνεται ( αν γίνεται ) με την περίπτωση που οι ρίζες της εξίσωσης είναι ίσες.
Εάν έχεις χρόνο και διαρκεί ακόμα το ενδιαφέρον σου για την άσκηση ,προσπάθησε να συμπληρώσεις αν θες την απάντηση σου .
 και
και  "
"  ή το
ή το  .
.Καλησπέρα σε όλους!nikkru έγραψε:Καλό απόγευμα Μιχάλη,maiksoul έγραψε:Καλημέρα nikkru (Νίκο;...)! Σε ευχαριστώ για τον χρόνο σου.Στην απάντηση σου έχω να παρατηρήσω τα εξής:
1) Στην λύση σου θεωρείς ότι οι (αρνητικές..όπως πολύ σωστά επισημαίνεις..) ρίζες τις εξίσωσης , είναι...διαφορετικές μεταξύ τους.Αυτό όμως δεν είναι το μοναδικό που μπορεί να συμβεί και ούτε προκύπτει αναγκαστικά από τα δεδομένα.
2)Πρέπει να συμπληρωθεί η λύση σου , με το τι γίνεται ( αν γίνεται ) με την περίπτωση που οι ρίζες της εξίσωσης είναι ίσες.
Εάν έχεις χρόνο και διαρκεί ακόμα το ενδιαφέρον σου για την άσκηση ,προσπάθησε να συμπληρώσεις αν θες την απάντηση σου .
Μάλλον καθένας μας ερμηνεύει διαφορετικά το " ακριβώς μια λύση", το οποίο νομίζω ότι είναι διαφορετικό από το " δύο ρίζες ίσες" .
'Έτσι, αφού η εξίσωση είναι δευτεροβάθμια και έχουμε δεδομένο " έχει ακριβώς μία λύση διαφορετική από τους αριθμούςκαι
"
άρα η εξίσωση έχει δύο λύσεις και μάλιστα η άλλη λύση της είναι τοή το
.
ΕίναιΓιώργος Ρίζος έγραψε:
Πάντως, θα χαρώ να δω..... το πρόσημο της Διακρίνουσας λυμένα με εργαλεία της Α΄ Λυκείου.



![D=\lambda ^{2}(\lambda +2)[(\lambda -1)^{3}+\lambda ^{2}+\lambda -3] D=\lambda ^{2}(\lambda +2)[(\lambda -1)^{3}+\lambda ^{2}+\lambda -3]](/forum/ext/geomar/texintegr/latexrender/pictures/0091b8002d17fd415a078c3507dd55a9.png)
 τότε
τότε 
 τότε
τότε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες