Συνευθειακότητα λόγω συμμετρίας

[KARKAR]

Συνευθειακότητα λόγω συμμετρίας.png (20.33 KiB) Προβλήθηκε 2085 φορές

Η διάμετρος του περικύκλου του τριγώνου τέμνει τη στο .

Έστω σημείο της , ώστε . Ο κύκλος τέμνει

τον κύκλο στο . Δείξτε ότι η διέρχεται από το .

[ealexiou]

Καλησπέρα!

Συνευθειακότητα λόγω συμμετρίας.png (22.4 KiB) Προβλήθηκε 2042 φορές

Αν μέσον του θα είναι και μέσον 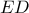και αφού μεσοκάθετος της χορδής μαύρου κύκλου θα είναι και μεσοκέθετος της χορδής 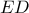του κόκκινου κύκλου και άρα το κέντρο του βρίσκεται πάνω στην προέκταση της της και άρα μεσοκάθετος της κοινής χορδής των δύο κύκλων και άρα συμμετρική της με άξονα συμμετρίας την και το ζητούμενο έπεται.
(Μόνο στην εισαγωγή υπάρχει σύμπτωση με την λύση του Γιώργου, γεια σου Γιώργο)

Λίγο διαφορετικά, αφού μεσοκάθετος της και αφού ( μέσον του) , άρα και .
Είναι (βαίνουν στο ίδιο τόξο ). Από και και άρα η διέρχεται από το .

Επεξεργασία: Πρόσθεσα την αιτιολόγηση.

[george visvikis]

Το συνημμένο Συνευθειακότητα λόγω συμμετρίας.png δεν είναι πλέον διαθέσιμο

Η διάμετρος του περικύκλου του τριγώνου τέμνει τη στο .

Έστω σημείο της , ώστε . Ο κύκλος τέμνει

τον κύκλο στο . Δείξτε ότι η διέρχεται από το .

Χαιρετώ τους φίλους!

Δεν ξέρω αν αυτό εννοεί ο Ευθύμης.

Συνευθειακότητα λόγω συμμετρίας.png (21.8 KiB) Προβλήθηκε 2019 φορές

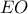Θα αποδείξω το ισοδύναμο πρόβλημα: Αν η τέμνει τον κύκλο στο , τότε το είναι εγγράψιμο.

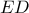Πράγματι, το μέσο της είναι και μέσο του κι επειδή , θα είναι . Αλλά , οπότε και , άρα το είναι ισοσκελές τραπέζιο, δηλαδή εγγράψιμο σε κύκλο.