Λίγο απ όλα και ομοκυκλικά
Συντονιστής: Μιχάλης Νάννος
Λίγο απ όλα και ομοκυκλικά
Δίνεται ορθογώνιο τρίγωνο ΑΒΓ με Α=90 μοίρες και ΑΒ<ΑΓ και το ύψος του ΑΔ. Αν Μ, Ε, Ζ είναι τα μέσα των πλευρών ΒΓ, ΑΓ, ΑΒ αντίστοιχα δείξτε οτι
α) Το Δ είναι μεταξύ Β και Μ
β) Το τετράπλευρο ΔΜΕΖ είναι ισοσκελές τραπέζιο
γ) Τα Α,Ζ,Δ,Μ,Ε είναι ομοκυκλικά
α) Το Δ είναι μεταξύ Β και Μ
β) Το τετράπλευρο ΔΜΕΖ είναι ισοσκελές τραπέζιο
γ) Τα Α,Ζ,Δ,Μ,Ε είναι ομοκυκλικά
Re: Λίγο απ όλα και ομοκυκλικά
α) Είναι  ,
,  και
και  επειδή τα τρίγωνα
επειδή τα τρίγωνα  και
και  έχουν
έχουν  κοινή
κοινή  (
( διάμεσος) και
διάμεσος) και  ,
,
οπότε και
και  γιατί
γιατί  και
και  παραπληρωματικές. Έτσι το τρίγωνο
παραπληρωματικές. Έτσι το τρίγωνο  είναι οξυγώνιο, οπότε το ύψος
είναι οξυγώνιο, οπότε το ύψος  είναι εσωτερικό του τριγώνου,
είναι εσωτερικό του τριγώνου,
δηλαδή το είναι μεταξύ των
είναι μεταξύ των  και
και  .
.
β) Κλασσικό.
 (1) ως διάμεσος στην υποτείνουσα
(1) ως διάμεσος στην υποτείνουσα 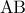 του ορθ.τριγώνου
του ορθ.τριγώνου  .
.
 (2) γιατί ενώνει τα μέσα των πλευρών
(2) γιατί ενώνει τα μέσα των πλευρών 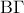 και
και  του τριγώνου
του τριγώνου  .
.
 (3) γιατί ενώνει τα μέσα των πλευρών
(3) γιατί ενώνει τα μέσα των πλευρών 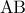 και
και  του τριγώνου
του τριγώνου  .
.
Από τις (1) , (2) , (3) συμπεραίνουμε ότι το είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.
γ) Αν είναι το μέσο της ΑΜ, τότε:
είναι το μέσο της ΑΜ, τότε:
 (4) ως διάμεσος στην υποτείνουσα
(4) ως διάμεσος στην υποτείνουσα  του ορθ.τριγώνου
του ορθ.τριγώνου 
 (5)
(5)
 (6) γιατί το
(6) γιατί το  ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  του τριγώνου
του τριγώνου  και
και  ως διάμεσος στην υποτείνουσα
ως διάμεσος στην υποτείνουσα 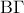 του ορθ.τριγώνου
του ορθ.τριγώνου  .
.
 (7) γιατί το
(7) γιατί το  ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  του τριγώνου
του τριγώνου  .
.
Από (4), (5), (6) και (7) είναι , δηλαδή τα σημεία
, δηλαδή τα σημεία  είναι ομοκυκλικά σε κύκλο με κέντρο το μέσο
είναι ομοκυκλικά σε κύκλο με κέντρο το μέσο  της διαμέσου
της διαμέσου  και ακτίνα
και ακτίνα 
 ,
,  και
και  επειδή τα τρίγωνα
επειδή τα τρίγωνα  και
και  έχουν
έχουν  κοινή
κοινή  (
( διάμεσος) και
διάμεσος) και  ,
, οπότε
 και
και  γιατί
γιατί  και
και  παραπληρωματικές. Έτσι το τρίγωνο
παραπληρωματικές. Έτσι το τρίγωνο  είναι οξυγώνιο, οπότε το ύψος
είναι οξυγώνιο, οπότε το ύψος  είναι εσωτερικό του τριγώνου,
είναι εσωτερικό του τριγώνου, δηλαδή το
 είναι μεταξύ των
είναι μεταξύ των  και
και  .
.β) Κλασσικό.
 (1) ως διάμεσος στην υποτείνουσα
(1) ως διάμεσος στην υποτείνουσα 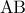 του ορθ.τριγώνου
του ορθ.τριγώνου  .
. (2) γιατί ενώνει τα μέσα των πλευρών
(2) γιατί ενώνει τα μέσα των πλευρών 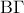 και
και  του τριγώνου
του τριγώνου  .
. (3) γιατί ενώνει τα μέσα των πλευρών
(3) γιατί ενώνει τα μέσα των πλευρών 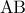 και
και  του τριγώνου
του τριγώνου  .
.Από τις (1) , (2) , (3) συμπεραίνουμε ότι το
 είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.γ) Αν
 είναι το μέσο της ΑΜ, τότε:
είναι το μέσο της ΑΜ, τότε: (4) ως διάμεσος στην υποτείνουσα
(4) ως διάμεσος στην υποτείνουσα  του ορθ.τριγώνου
του ορθ.τριγώνου 
 (5)
(5) (6) γιατί το
(6) γιατί το  ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  του τριγώνου
του τριγώνου  και
και  ως διάμεσος στην υποτείνουσα
ως διάμεσος στην υποτείνουσα 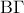 του ορθ.τριγώνου
του ορθ.τριγώνου  .
. (7) γιατί το
(7) γιατί το  ενώνει τα μέσα των πλευρών
ενώνει τα μέσα των πλευρών  του τριγώνου
του τριγώνου  .
.Από (4), (5), (6) και (7) είναι
 , δηλαδή τα σημεία
, δηλαδή τα σημεία  είναι ομοκυκλικά σε κύκλο με κέντρο το μέσο
είναι ομοκυκλικά σε κύκλο με κέντρο το μέσο  της διαμέσου
της διαμέσου  και ακτίνα
και ακτίνα 
- Συνημμένα
-
- Ορθ. Τριγωνο.png (21.76 KiB) Προβλήθηκε 552 φορές
τελευταία επεξεργασία από hlkampel σε Πέμ Ιούλ 14, 2011 7:42 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Ηλίας Καμπελής
- Καρδαμίτσης Σπύρος
- Επιμελητής
- Δημοσιεύσεις: 2338
- Εγγραφή: Κυρ Δεκ 21, 2008 11:14 pm
- Επικοινωνία:
Re: Λίγο απ όλα και ομοκυκλικά
Tα α και γ ερωτήματα με διαφορετικό τρόπο, το β με τον ίδιο.
α) Είναι συνεπώς το τρίγωνο
συνεπώς το τρίγωνο  είναι ισοσκελές άρα
είναι ισοσκελές άρα
 και
και 
Έστω ότι:

άρα είναι , άτοπο,
, άτοπο,
επομένως είναι
 ,
,
συνεπώς το σημείο Δ βρίσκεται μεταξύ των Β και Μ.
β) Τα σημεία Ε και Ζ είναι μέσα πλευρών, συνεπώς , άρα το τετράπλευρο
, άρα το τετράπλευρο  είναι τραπέζιο.
είναι τραπέζιο.
Επιπλέον, τα σημεία Ε και Μ είναι μέσα πλευρών άρα (1) .
(1) .
Ακόμη στο τρίγωνο η
η  είναι διάμεσός του άρα
είναι διάμεσός του άρα  (2)
(2)
Από τις σχέσεις (1) και (2) έχουμε ότι , άρα το τραπέζιο
, άρα το τραπέζιο  είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.
γ) Τα τρίγωνα και
και  είναι ίσα (γιατί
είναι ίσα (γιατί  ,
,  ,
,  ως διαγώνιες ισοσκελούς τραπεζίου ) ,
ως διαγώνιες ισοσκελούς τραπεζίου ) ,
επιπλέον είναι αφού το τετράπλευρο
αφού το τετράπλευρο  είναι ορθογώνιο , άρα οι γωνίες
είναι ορθογώνιο , άρα οι γωνίες
 ,
,  και
και 
βλέπουν υπό ορθή γωνία την ,
,
άρα τα σημεία είναι ομοκυκλικά.
είναι ομοκυκλικά.
α) Είναι
 συνεπώς το τρίγωνο
συνεπώς το τρίγωνο  είναι ισοσκελές άρα
είναι ισοσκελές άρα  και
και 
Έστω ότι:

άρα είναι
 , άτοπο,
, άτοπο, επομένως είναι
 ,
, συνεπώς το σημείο Δ βρίσκεται μεταξύ των Β και Μ.
β) Τα σημεία Ε και Ζ είναι μέσα πλευρών, συνεπώς
 , άρα το τετράπλευρο
, άρα το τετράπλευρο  είναι τραπέζιο.
είναι τραπέζιο. Επιπλέον, τα σημεία Ε και Μ είναι μέσα πλευρών άρα
 (1) .
(1) . Ακόμη στο τρίγωνο
 η
η  είναι διάμεσός του άρα
είναι διάμεσός του άρα  (2)
(2)Από τις σχέσεις (1) και (2) έχουμε ότι
 , άρα το τραπέζιο
, άρα το τραπέζιο  είναι ισοσκελές τραπέζιο.
είναι ισοσκελές τραπέζιο.γ) Τα τρίγωνα
 και
και  είναι ίσα (γιατί
είναι ίσα (γιατί  ,
,  ,
,  ως διαγώνιες ισοσκελούς τραπεζίου ) ,
ως διαγώνιες ισοσκελούς τραπεζίου ) ,επιπλέον είναι
 αφού το τετράπλευρο
αφού το τετράπλευρο  είναι ορθογώνιο , άρα οι γωνίες
είναι ορθογώνιο , άρα οι γωνίες  ,
,  και
και 
βλέπουν υπό ορθή γωνία την
 ,
, άρα τα σημεία
 είναι ομοκυκλικά.
είναι ομοκυκλικά.- Συνημμένα
-
- λίγο απ΄ολα και ομοκυκλικά.PNG (15.21 KiB) Προβλήθηκε 528 φορές
Καρδαμίτσης Σπύρος
- Stavroulitsa
- Δημοσιεύσεις: 455
- Εγγραφή: Τρί Ιούλ 14, 2009 1:44 pm
- Τοποθεσία: Θεσσαλονίκη (Πολίχνη)
Re: Λίγο απ όλα και ομοκυκλικά
Καλησπέρα! Θα πω μια διαφορετική σκέψη για το 1ο ερώτημα...
έχουμε ΑΓ>ΑΒ άρα θα ισχύει

και αναγκαστικά το μέσο Μ θα βρίσκεται στο ευγύγραμμο τμήμα ΔΓ...
έχουμε ΑΓ>ΑΒ άρα θα ισχύει

και αναγκαστικά το μέσο Μ θα βρίσκεται στο ευγύγραμμο τμήμα ΔΓ...
"Millions long for immortality who do not know what to do with themselves on a rainy Sunday afternoon"
Susan Ertz
Susan Ertz
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
