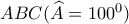 θεωρούμε σημείο
θεωρούμε σημείο  ώστε
ώστε 
και
 Να υπολογίσετε τη γωνία
Να υπολογίσετε τη γωνία 
Συντονιστής: Μιχάλης Νάννος
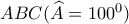 θεωρούμε σημείο
θεωρούμε σημείο  ώστε
ώστε 
 Να υπολογίσετε τη γωνία
Να υπολογίσετε τη γωνία 
 με τη δοθείσα ιδιότητα.
με τη δοθείσα ιδιότητα. επί της διχοτόμου της
επί της διχοτόμου της  τέτοιο ώστε
τέτοιο ώστε  και
και  το συμμετρικό του
το συμμετρικό του  ως προς την
ως προς την  .
. και
και  , άρα το
, άρα το 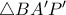 είναι ισόπλευρο.
είναι ισόπλευρο.  και αφού
και αφού  , έπεται ότι
, έπεται ότι 
 και κατά συνέπεια
και κατά συνέπεια  . Άρα
. Άρα  και
και  .
. . Συνεπώς λόγω της μοναδικότητας
. Συνεπώς λόγω της μοναδικότητας  και
και 
 του ισοσκελούς
του ισοσκελούς  που είναι διχοτόμος και ύψος.
που είναι διχοτόμος και ύψος. τέμνει την
τέμνει την  στο
στο  .
. ( έμμεσο κριτήριο) και συνεπώς :
( έμμεσο κριτήριο) και συνεπώς : .
.
 έχουν :
έχουν : 
 που προφανώς
που προφανώς 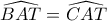 κι αφού έχουν άθροισμα
κι αφού έχουν άθροισμα  θα
θα 
 του τριγώνου
του τριγώνου  .
. ,
,  , και αφού
, και αφού  ,
,  (1).
(1). έχουν κοινή πλευρά
έχουν κοινή πλευρά  και είναι ισοσκελή (αφού
και είναι ισοσκελή (αφού  , από υπόθεση, και
, από υπόθεση, και  λόγω του περικέντρου).
λόγω του περικέντρου).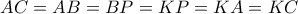 , οπότε το
, οπότε το  είναι ισόπλευρο.
είναι ισόπλευρο.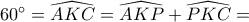
 .
. του
του  ως προς την
ως προς την  .
. , οπότε
, οπότε 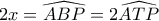 , και αφού
, και αφού  , το
, το  είναι περίκεντρο του
είναι περίκεντρο του 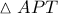 και
και  , οπότε το
, οπότε το  είναι ισόπλευρο.
είναι ισόπλευρο.
 .
. ,
,  , και από το ισοσκελές
, και από το ισοσκελές  ,
, .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 22 επισκέπτες