Ίσον προς το ήμισυ Τετράπλευρου

kostasrmd · #1

Να δειχθεί ότι το τετράπλευρο που έχει κορυφές τα μέσα των πλευρών ετέρου τετραπλεύρου ισούται προς το ήμισυ αυτού.
Γνώμη για την άσκηση;(βαθμός δυσκολίας).

#2

kostasrmd έγραψε: ↑
Τρί Δεκ 26, 2017 7:50 pm
Να δειχθεί ότι το τετράπλευρο που έχει κορυφές τα μέσα των πλευρών ετέρου τετραπλεύρου ισούται προς το ήμισυ αυτού.
Γνώμη για την άσκηση;(βαθμός δυσκολίας).

Φαντάζομαι ότι αναφέρεσαι στα εμβαδά των τετραπλεύρων.

Απλή, θα έλεγα, ενδιαφέρουσα σχολική άσκηση, εφαρμογή βασικών ιδιοτήτων. Όμως δεν αφορά μόνο την ύλη της Α΄ Λυκείου, αλλά και της Β' (εμβαδά). Σχετίζεται με τις ενότητες: 5.6 και 10.5 της σχολικής γεωμετρίας.

hlkampel · #3

kostasrmd έγραψε: ↑
Τρί Δεκ 26, 2017 7:50 pm
Να δειχθεί ότι το τετράπλευρο που έχει κορυφές τα μέσα των πλευρών ετέρου τετραπλεύρου ισούται προς το ήμισυ αυτού.
Γνώμη για την άσκηση;(βαθμός δυσκολίας).

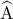Από την ομοιότητα των τριγώνων ${\rm A}{\rm E}\Theta$ και ${\rm A}{\rm B}\Delta$ ( $\widehat {\rm A}$ κοινή και ${\rm E}\Theta //{\rm B}\Delta$ ) με λόγο ομοιότητας $\frac{1}{2}$ είναι $\left( {{\rm A}{\rm E}\Theta } \right) = \dfrac{1}{4}\left( {{\rm A}{\rm B}\Delta } \right)$ .

Ομοίως $\left( {\Gamma {\rm Z}{\rm H}} \right) = \dfrac{1}{4}\left( {{\rm B}\Gamma \Delta } \right)$ , $\left( {{\rm E}{\rm B}{\rm Z}} \right) = \dfrac{1}{4}\left( {{\rm A}{\rm B}\Gamma } \right)$ και $\left( {\Theta \Delta {\rm H}} \right) = \dfrac{1}{4}\left( {{\rm A}\Delta \Gamma } \right)$

Με πρόσθεση κατά μέλη παίρνουμε:

$\left( {{\rm A}{\rm E}\Theta } \right) + \left( {\Gamma {\rm Z}{\rm H}} \right) + \left( {{\rm E}{\rm B}{\rm Z}} \right) + \left( {\Theta \Delta {\rm H}} \right) = \dfrac{1}{2}\left( {{\rm A}{\rm B}\Gamma \Delta } \right) \Leftrightarrow$

$\left( {{\rm E}{\rm Z}{\rm H}\Theta } \right) = \dfrac{1}{2}\left( {{\rm A}{\rm B}\Gamma \Delta } \right)$

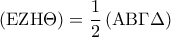
Σημείωση: Την θεωρώ εύκολη και κλασσική για την Β' Λυκείου (εκεί έχουν τα εμβαδά).

Edit: Έδωσε ο Γιώργος απάντηση. Την αφήνω για την λύση...

KARKAR · #4

Για να θυμίσουμε το διεθνές όνομα του θεωρήματος , ας πάμε εδώ

#5

Και μια λύση ακόμη

: Εμβαδον μεσοπλεύρου.png (24.63 KiB) Προβλήθηκε 1137 φορές

$\left\{ \begin{gathered} (ABCD) = (ABD) + (CBD) = 2kd + 2ku = 2k(d + u) \hfill \\ (EZHT) = k(d + u) \hfill \\ \end{gathered} \right. \Rightarrow (ABCD) = 2(EZHT)$

Θα έλεγα βασική άσκηση .

kostasrmd · #6

Γιώργος Ρίζος έγραψε: ↑
Τρί Δεκ 26, 2017 8:26 pm

kostasrmd έγραψε: ↑
Τρί Δεκ 26, 2017 7:50 pm
Να δειχθεί ότι το τετράπλευρο που έχει κορυφές τα μέσα των πλευρών ετέρου τετραπλεύρου ισούται προς το ήμισυ αυτού.
Γνώμη για την άσκηση;(βαθμός δυσκολίας).
Φαντάζομαι ότι αναφέρεσαι στα εμβαδά των τετραπλεύρων.

Απλή, θα έλεγα, ενδιαφέρουσα σχολική άσκηση, εφαρμογή βασικών ιδιοτήτων. Όμως δεν αφορά μόνο την ύλη της Α΄ Λυκείου, αλλά και της Β' (εμβαδά). Σχετίζεται με τις ενότητες: 5.6 και 10.5 της σχολικής γεωμετρίας.

Καλησπέρα Γιώργο!.Ο λόγοι που δημοσίευσα αυτήν την άσκηση στην κατηγορία Α' Λυκείου ήταν ,πρώτον, επειδή το βιβλίο από όπου την πήρα(παλαιό βοήθημα Γεωμετρίας) την είχε στο κεφάλαιο με τα παραλληλογραμμα, δηλαδή πολύ πριν τα εμβαδά(τουλάχιστον από ότι θυμάμαι από το λύκειο), και, δεύτερον, επειδή για να λυθεί δεν χρειάζεται κάποιος τύπος εμβαδού σχήματος άλλα μόνο ισότητα τριγώνων. Παραθέτω την λύση του συγκεκριμενου βοηθήματος:

Προεκτείνω τις UH, EZ

κατά ίσα τμήματα HU',ZE'

οπότε το παραλληλογραμμο HU'E'Z

είναι ίσο προς το αρχικό. Από την ισότητα των τριγώνων( UDH,HU'G

), (

) , (

) προκύπτει το ζητούμενο.

KARKAR · #7

: Varignon.png (17.75 KiB) Προβλήθηκε 1102 φορές

Η ωραιότατη λύση που παραθέτει ο θεματοδότης , με βάζει σε πειρασμό να προτείνω το εξής :

Έστω σημείο

στο εσωτερικό του τετραπλεύρου , έτσι ώστε το AKSN

να είναι

παραλληλόγραμμο . Αν αποδειχθεί ότι και το CMSL

είναι παραλληλόγραμμο τότε ,

λόγω και των ισοτήτων των μαύρων και των λευκών τριγώνων , τελειώσαμε !

kostasrmd · #8

KARKAR έγραψε: ↑
Τετ Δεκ 27, 2017 11:22 am
Varignon.pngΗ ωραιότατη λύση που παραθέτει ο θεματοδότης , με βάζει σε πειρασμό να προτείνω το εξής :

Έστω σημείο στο εσωτερικό του τετραπλεύρου , έτσι ώστε το να είναι

παραλληλόγραμμο . Αν αποδειχθεί ότι και το είναι παραλληλόγραμμο τότε ,

λόγω και των ισοτήτων των μαύρων και των λευκών τριγώνων , τελειώσαμε !

Έχουμε ότι KS=AN=ND(1), KL=NM

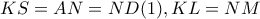(2) λόγω των παραλληλογραμμων ANKS, ABCD

αντίστοιχα. Προεκτεινουμε την

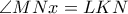όποτε σχηματίζεται η $\angle MNx=LKN$ .Έχουμε διαδοχικά ότι 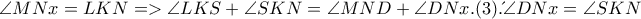$\angle MNx=LKN=>\angle LKS+\angle SKN=\angle MND+\angle DNx.(3).Επειδή \angle DNx=\angle SKN$ από την (3) προκύπτει ότι $\angle LKS=\angle MND$ και ,λογω των (1),(2) ,τα τρίγωνα KLS,MND

είναι ίσα. Ομοίως εργαζόμενοι αποδεικνυουμε και την ισότητα των KBL,NSM

.Εκ των δυο ισοτήτων τρίγωνων συνάγουμε ότι το τετράπλευρο SLCM

έχει τις απέναντι πλευρές του ίσες, συνεπώς είναι παραλληλογραμμο, άρα και τα τρίγωνα LCM,LSM

είναι ίσα το οποίο αποδεικνύει το ζητούμενο.
Σωστο ή εχω καπου λαθος; Σημειωνω οτι εχω τελειωσει το λυκειο εδω και μερικα χρονια απλως ασχολουμαι στον ελευθερο χρονο μου με τα Μαθηματικα, οποτε τυχον λαθη ή απροσεξιες ζητω να γινουν κατανοητα.

Ίσον προς το ήμισυ Τετράπλευρου

Ίσον προς το ήμισυ Τετράπλευρου

Re: Ίσον προς το ήμισυ Τετράπλευρου

Re: Ίσον προς το ήμισυ Τετράπλευρου

Re: Ίσον προς το ήμισυ Τετράπλευρου

Re: Ίσον προς το ήμισυ Τετράπλευρου

Re: Ίσον προς το ήμισυ Τετράπλευρου

Re: Ίσον προς το ήμισυ Τετράπλευρου

Re: Ίσον προς το ήμισυ Τετράπλευρου

Μέλη σε σύνδεση