 του σχήματος , το ορθόκεντρο
του σχήματος , το ορθόκεντρο  ανήκει στο τμήμα
ανήκει στο τμήμα  , το οποίο
, το οποίοενώνει τα μέσα των πλευρών
 . Βρείτε τρόπους κατασκευής τέτοιων τριγώνων .
. Βρείτε τρόπους κατασκευής τέτοιων τριγώνων .Συντονιστής: Μιχάλης Νάννος
 του σχήματος , το ορθόκεντρο
του σχήματος , το ορθόκεντρο  ανήκει στο τμήμα
ανήκει στο τμήμα  , το οποίο
, το οποίο . Βρείτε τρόπους κατασκευής τέτοιων τριγώνων .
. Βρείτε τρόπους κατασκευής τέτοιων τριγώνων . .
.Με διάμετρο τυχαίο τμήμα
 γράφω ημικύκλιο . Έστω τυχαίο του σημείο
γράφω ημικύκλιο . Έστω τυχαίο του σημείο  .
. και θεωρώ το συμμετρικό,
και θεωρώ το συμμετρικό,  , του
, του  ως προς
ως προς  .
Η από το
.
Η από το  παράλληλη στην
παράλληλη στην  τέμνει την
τέμνει την  στο
στο  και την
και την  στο
στο  .
. είναι αυτό που θέλω.
είναι αυτό που θέλω. .
. στο
στο  , το
, το  στο
στο  και κατασκευάζουμε τις ευθείες
και κατασκευάζουμε τις ευθείες 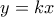 και
και  . Αν
. Αν  το σημείο τομής τους, το τρίγωνο
το σημείο τομής τους, το τρίγωνο  ικανοποιεί το ζητούμενο. (Υπάρχουν άπειρες τιμές του
ικανοποιεί το ζητούμενο. (Υπάρχουν άπειρες τιμές του  που η κατασκευή γίνεται με κανόνα και διαβήτη.)
που η κατασκευή γίνεται με κανόνα και διαβήτη.)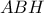 είναι
είναι  .
. .
. , επομένως θέλουμε
, επομένως θέλουμε  .
. , παίρνουμε
, παίρνουμε  .
. κλπ...
κλπ... .
. .
. στο σημείο
στο σημείο  και παίρνω σημείο
και παίρνω σημείο  σε αυτήν την κάθετη.
σε αυτήν την κάθετη. το μέσο του
το μέσο του  .
. το σημείο τομής της
το σημείο τομής της  με την κάθετη από το
με την κάθετη από το  στην
στην  .
.  και άρα η κατασκευή ικανοποιεί το ζητούμενο.
και άρα η κατασκευή ικανοποιεί το ζητούμενο.Με βάση την ημετέρα κατασκευήDemetres έγραψε: ↑Τετ Σεπ 06, 2023 9:19 amΔείξτε ότι αυτό συμβαίνει αν και μόνο αν.
Αυτό μπορεί να μας δώσει και τρόπους κατασκευής. Τοποθετούμε π.χ. τοστο
, το
στο
και κατασκευάζουμε τις ευθείες
και
. Αν
το σημείο τομής τους, το τρίγωνο
ικανοποιεί το ζητούμενο. (Υπάρχουν άπειρες τιμές του
που η κατασκευή γίνεται με κανόνα και διαβήτη.)
 που ισχύει γιατί :
που ισχύει γιατί :  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες