
1) Να βρείτε το πεδίο ορισμού της.
2) Αν
 , να βρείτε το
, να βρείτε το  .
.3) Αν
 , τότε:
, τότε:i. να λύσετε στο διάστημα
 την εξίσωση:
την εξίσωση: 
ii. να λύσετε την εξίσωση

iii. να λύστετε την ανίσωση

Συντονιστής: exdx

 , να βρείτε το
, να βρείτε το  .
. , τότε:
, τότε: την εξίσωση:
την εξίσωση: 


α) Πρέπειerxmer έγραψε:Δίνεται η συνάρτηση
1) Να βρείτε το πεδίο ορισμού της.
2) Αν, να βρείτε το
.
3) Αν, τότε:
i. να λύσετε στο διάστηματην εξίσωση:
ii. να λύσετε την εξίσωση
iii. να λύστετε την ανίσωση
 . Άρα το σύνολο ορισμού της
. Άρα το σύνολο ορισμού της  είναι το
είναι το 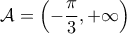 .
. γ) Για
γ) Για  έχουμε
έχουμε  άρα:
άρα:
 Λόγω πεδίο ορισμού θα πρέπει να ισχύει
Λόγω πεδίο ορισμού θα πρέπει να ισχύει  . Συνεπώς
. Συνεπώς  .
.![\displaystyle{\begin{aligned}
f(x) \geq f^2 (x) - 2 &\Leftrightarrow \ln \left ( x + \frac{\pi}{3} \right ) +1 \geq \left [ \ln \left ( x + \frac{\pi}{3} \right ) + 1 \right ]^2 -2 \\
&\Leftrightarrow \ln \left ( x + \frac{\pi}{3} \right ) + 1 \geq \ln^2 \left ( x + \frac{\pi}{3} \right ) + 2 \ln \left ( x + \frac{\pi}{3} \right ) + 1 -2 \\
&\Leftrightarrow \ln^2 \left ( x + \frac{\pi}{3} \right ) + \ln \left ( x + \frac{\pi}{3} \right ) - 2 \leq 0 \\
&\!\!\!\!\!\!\!\!\!\!\overset{y= \ln \left ( x + \frac{\pi}{3} \right )}{\Leftarrow\!=\! =\! =\!=\! =\! \Rightarrow} y^2 + y -2 \leq 0 \\
&\Leftrightarrow - 2 \leq y \leq 1 \\
&\Leftrightarrow -2 \leq \ln \left ( x + \frac{\pi}{3} \right ) \leq 1 \\
&\Leftrightarrow x \in \left [ \frac{1}{e^2} - \frac{\pi}{3} , e - \frac{\pi}{3} \right ]
\end{aligned}} \displaystyle{\begin{aligned}
f(x) \geq f^2 (x) - 2 &\Leftrightarrow \ln \left ( x + \frac{\pi}{3} \right ) +1 \geq \left [ \ln \left ( x + \frac{\pi}{3} \right ) + 1 \right ]^2 -2 \\
&\Leftrightarrow \ln \left ( x + \frac{\pi}{3} \right ) + 1 \geq \ln^2 \left ( x + \frac{\pi}{3} \right ) + 2 \ln \left ( x + \frac{\pi}{3} \right ) + 1 -2 \\
&\Leftrightarrow \ln^2 \left ( x + \frac{\pi}{3} \right ) + \ln \left ( x + \frac{\pi}{3} \right ) - 2 \leq 0 \\
&\!\!\!\!\!\!\!\!\!\!\overset{y= \ln \left ( x + \frac{\pi}{3} \right )}{\Leftarrow\!=\! =\! =\!=\! =\! \Rightarrow} y^2 + y -2 \leq 0 \\
&\Leftrightarrow - 2 \leq y \leq 1 \\
&\Leftrightarrow -2 \leq \ln \left ( x + \frac{\pi}{3} \right ) \leq 1 \\
&\Leftrightarrow x \in \left [ \frac{1}{e^2} - \frac{\pi}{3} , e - \frac{\pi}{3} \right ]
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/5ad0abd69d6ce1035e545b9bd10684fd.png)

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες