
Σύστημα!
Συντονιστής: exdx
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Σύστημα!
Καλό.Ορέστης Λιγνός έγραψε:Να λύσετε στους πραγματικούς αριθμούς το σύστημα
Δεδομένου ότι έπεται
 και άρα
και άρα  και όμοια για το
και όμοια για το  , μπορούμε να θέσουμε
, μπορούμε να θέσουμε  (το
(το  στο σωστό τεταρτημόριο).
στο σωστό τεταρτημόριο). H δεύτερη εξίσωση γίνεται διαδοχικά
 ,
, άρα
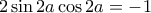 , οπότε
, οπότε  . Τώρα η εύρεση του
. Τώρα η εύρεση του  είναι απλή, και λοιπά.
είναι απλή, και λοιπά.- Tolaso J Kos
- Δημοσιεύσεις: 5227
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Σύστημα!
Επιχειρώ μία λύση με τριγωνομετρία και επειδή είναι η πρώτη φορά που το κάνω θα θελα τη γνώμη μου κοινού.Ορέστης Λιγνός έγραψε:Να λύσετε στους πραγματικούς αριθμούς το σύστημα
Επειδή η πρώτη εξίσωση είναι κύκλος εύλογο είναι να θέσουμε
 και
και  με
με  . Τότε η δεύτερη εξίσωση γίνεται:
. Τότε η δεύτερη εξίσωση γίνεται: Άρα
Άρα  και
και 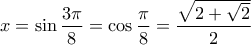 και τέλος
και τέλος  αλλά και
αλλά και  . Άρα το σύστημα έχει τέσσερις λύσεις.
. Άρα το σύστημα έχει τέσσερις λύσεις. Με μία επαλήθευση με το Wolfram σωστά φαίνεται να τις έχω βρει. Ενδιάφερον έχει να βρεθεί και αλγεβρική επίλυση. Οι παραπάνω τριγωνομετρικοί αριθμοί θεωρούνται γνωστοί και τους έχουμε δει πάμπολες φορές στο
Ουπς: ήρθα δεύτερος. Το αφήνω διότι έχω δώσει και τις λύσεις.
Η φαντασία είναι σημαντικότερη από τη γνώση !


- exdx
- Επιμελητής
- Δημοσιεύσεις: 1742
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Σύστημα!
Με τον κλασικό τρόπο , επειδή είναι ομογενές ως προς  και
και 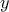
Θέτω ,
, 
Τότε το σύστημα γίνεται


Έπονται οι αντικαταστάσεις για την εύρεση των
 και
και 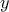
Θέτω
 ,
, 
Τότε το σύστημα γίνεται


Έπονται οι αντικαταστάσεις για την εύρεση των

Kαλαθάκης Γιώργης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες
