 =
= ![\sqrt[3]{16-2^x}+\sqrt{2 \cdot 3^x-18} \sqrt[3]{16-2^x}+\sqrt{2 \cdot 3^x-18}](/forum/ext/geomar/texintegr/latexrender/pictures/154895b896a453a6e0ea4b5ca66ea0e2.png) .
.α) Να βρείτε το πεδίο ορισμού της
 .
.β) Να λύσετε την ανίσωση
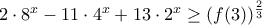
γ) Να λύσετε την εξίσωση
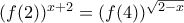
Μου άρεσε αυτή η άσκηση διότι μου υπενθύμισε πως οι συναρτήσεις δεν υπάρχουν μόνο στην Γ' Λυκείου!
Συντονιστής: exdx
 =
= ![\sqrt[3]{16-2^x}+\sqrt{2 \cdot 3^x-18} \sqrt[3]{16-2^x}+\sqrt{2 \cdot 3^x-18}](/forum/ext/geomar/texintegr/latexrender/pictures/154895b896a453a6e0ea4b5ca66ea0e2.png) .
. .
.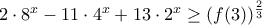
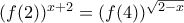
(α) Πρέπει
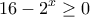 και
και 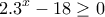 , από όπου προκύπτει ότι το πεδίο ορισμού της
, από όπου προκύπτει ότι το πεδίο ορισμού της  είναι το
είναι το ![\displaystyle{A=[2 , 4]} \displaystyle{A=[2 , 4]}](/forum/ext/geomar/texintegr/latexrender/pictures/c160903deff7b4483695957fed098bdc.png)
 , ή χωρίς να είναι απαραίτητο να είναι
, ή χωρίς να είναι απαραίτητο να είναι  )
)
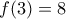 , άρα
, άρα 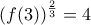
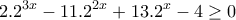 .
.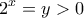 , και έχουμε:
, και έχουμε: 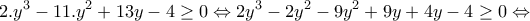
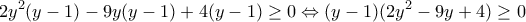 .
. 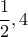 και δεδομένου ότι είναι και
και δεδομένου ότι είναι και 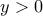 , κατασκευάζοντας τον πίνακα,
, κατασκευάζοντας τον πίνακα, ![\displaystyle{y\in [\frac{1}{2} , 1]U[4,+ \propto )} \displaystyle{y\in [\frac{1}{2} , 1]U[4,+ \propto )}](/forum/ext/geomar/texintegr/latexrender/pictures/3f97ad9cfb0368501c04b23ed960f1d1.png) και αφού
και αφού 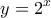 , παίρνουμε ότι
, παίρνουμε ότι ![\displaystyle{x\in[-1 ,0]U[2,+\propto)} \displaystyle{x\in[-1 ,0]U[2,+\propto)}](/forum/ext/geomar/texintegr/latexrender/pictures/20bf7a82d4ef309fc6306a72c3a847b4.png)
 , τότε έχουμε
, τότε έχουμε ![\displaystyle{x\in [2,4]} \displaystyle{x\in [2,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/13827eceffc6a222adacadb0eb902d85.png) )
)![\displaystyle{f(2)=\sqrt[3]{12}} \displaystyle{f(2)=\sqrt[3]{12}}](/forum/ext/geomar/texintegr/latexrender/pictures/e1b6fec490ad089682ab1dba804b2846.png) και
και 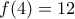
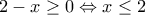
![\displaystyle{(\sqrt[3]{12})^{x+2} =12^{\sqrt{2-x}}\Leftrightarrow \frac{x+2}{3}=\sqrt{2-x}} \displaystyle{(\sqrt[3]{12})^{x+2} =12^{\sqrt{2-x}}\Leftrightarrow \frac{x+2}{3}=\sqrt{2-x}}](/forum/ext/geomar/texintegr/latexrender/pictures/c4f62b045858d7657aacd2957f3da017.png) , (1)
, (1)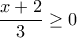 , δηλαδή
, δηλαδή 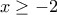 και αφού είχαμε και
και αφού είχαμε και 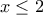 , τελικά θα
, τελικά θα 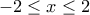 .
. 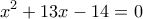 , της οποίας η μόνη δεκτή ρίζα είναι η
, της οποίας η μόνη δεκτή ρίζα είναι η  .
. , δηλαδή όταν
, δηλαδή όταν ![\displaystyle{x\in [2 ,4]} \displaystyle{x\in [2 ,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/9e69e6c173e4575732ab28e9e50075b5.png) , τότε πολύ πιο εύκολα, αφού είναι και
, τότε πολύ πιο εύκολα, αφού είναι και 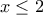 , έχουμε σαν μόνη πιθανή λύση την
, έχουμε σαν μόνη πιθανή λύση την  , η οποία όμως δεν επαληθεύει την εξίσωση μας και άρα η εξίσωση
, η οποία όμως δεν επαληθεύει την εξίσωση μας και άρα η εξίσωση Πολύ σωστά. Είναι, όμως, απαραίτητο να πάρουμε περιορισμούς σε κυβική ρίζα; Ποια είναι η άποψή σας; Ρώτησα τον καθηγητή μου και μου είπε πως θα το ερευνήσει ο ίδιος.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Δεκ 20, 2023 7:53 pm(α) Πρέπεικαι
, από όπου προκύπτει ότι το πεδίο ορισμού της
είναι το
(β). (Δεν ξέρω αν η άσκηση ζητάει να βρούμε λύση με, ή χωρίς να είναι απαραίτητο να είναι
)
Ας βρούμε λύση για όλες τις δυνατές τιμές του πραγματικού αριθμού
Έχουμε, άρα
Τώρα η δοσμένη ανίσωση γράφεται:.
Θέτουμε, και έχουμε:
.
Οι ρίζες του τριωνύμου είναικαι δεδομένου ότι είναι και
, κατασκευάζοντας τον πίνακα,
βρίσκουμε ότικαι αφού
, παίρνουμε ότι
(ΣΗΜΕΙΩΣΗ: Αν θέλουμε να βρούμε λύσεις όταν, τότε έχουμε
)
(γ) Είναικαι
Αρχικά πρέπει
Τώρα η δοσμένη εξίσωση γράφεται:, (1)
Πρέπει επί πλέον να είναι, δηλαδή
και αφού είχαμε και
, τελικά θα
πρέπει.
Υψώνοντας τα μέλη της (1) στο τετράγωνο παίρνουμε την εξίσωση:, της οποίας η μόνη δεκτή ρίζα είναι η
.
(ΣΗΜΕΙΩΣΗ: Αν θέλουμε να βρούμε λύσεις όταν, δηλαδή όταν
, τότε πολύ πιο εύκολα, αφού είναι και
, έχουμε σαν μόνη πιθανή λύση την
, η οποία όμως δεν επαληθεύει την εξίσωση μας και άρα η εξίσωση
είναι αδύνατη.)
Παλαιότερα, και στην Ελλάδα, τις κυβικές ρίζες (και γενικότερα οι περιττής τάξεως ρίζες), τις ορίζαμε και όταν η υπόριζη ποσότηταVenizelos έγραψε: ↑Τετ Δεκ 20, 2023 7:58 pmΠολύ σωστά. Είναι, όμως, απαραίτητο να πάρουμε περιορισμούς σε κυβική ρίζα; Ποια είναι η άποψή σας; Ρώτησα τον καθηγητή μου και μου είπε πως θα το ερευνήσει ο ίδιος.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Δεκ 20, 2023 7:53 pm(α) Πρέπεικαι
, από όπου προκύπτει ότι το πεδίο ορισμού της
είναι το
(β). (Δεν ξέρω αν η άσκηση ζητάει να βρούμε λύση με, ή χωρίς να είναι απαραίτητο να είναι
)
Ας βρούμε λύση για όλες τις δυνατές τιμές του πραγματικού αριθμού
Έχουμε, άρα
Τώρα η δοσμένη ανίσωση γράφεται:.
Θέτουμε, και έχουμε:
.
Οι ρίζες του τριωνύμου είναικαι δεδομένου ότι είναι και
, κατασκευάζοντας τον πίνακα,
βρίσκουμε ότικαι αφού
, παίρνουμε ότι
(ΣΗΜΕΙΩΣΗ: Αν θέλουμε να βρούμε λύσεις όταν, τότε έχουμε
)
(γ) Είναικαι
Αρχικά πρέπει
Τώρα η δοσμένη εξίσωση γράφεται:, (1)
Πρέπει επί πλέον να είναι, δηλαδή
και αφού είχαμε και
, τελικά θα
πρέπει.
Υψώνοντας τα μέλη της (1) στο τετράγωνο παίρνουμε την εξίσωση:, της οποίας η μόνη δεκτή ρίζα είναι η
.
(ΣΗΜΕΙΩΣΗ: Αν θέλουμε να βρούμε λύσεις όταν, δηλαδή όταν
, τότε πολύ πιο εύκολα, αφού είναι και
, έχουμε σαν μόνη πιθανή λύση την
, η οποία όμως δεν επαληθεύει την εξίσωση μας και άρα η εξίσωση
είναι αδύνατη.)
![\displaystyle{\sqrt[3]{x}} \displaystyle{\sqrt[3]{x}}](/forum/ext/geomar/texintegr/latexrender/pictures/d42c322967578eb2ab34690d60c1ad4b.png) έχει νόημα και όταν
έχει νόημα και όταν  , αλλά στα σχολικά δεδομένα
, αλλά στα σχολικά δεδομένα .
.Ευχαριστώ πολύ για τη διευκρίνιση! Αυτή ή άσκηση, θεωρείτε, θα μπορούσε να "πέσει" στις προαγωγικές της Β' Λυκείου ως κάποια υπερωτήματα;ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Δεκ 20, 2023 8:13 pmΠαλαιότερα, και στην Ελλάδα, τις κυβικές ρίζες (και γενικότερα οι περιττής τάξεως ρίζες), τις ορίζαμε και όταν η υπόριζη ποσότηταVenizelos έγραψε: ↑Τετ Δεκ 20, 2023 7:58 pmΠολύ σωστά. Είναι, όμως, απαραίτητο να πάρουμε περιορισμούς σε κυβική ρίζα; Ποια είναι η άποψή σας; Ρώτησα τον καθηγητή μου και μου είπε πως θα το ερευνήσει ο ίδιος.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Δεκ 20, 2023 7:53 pm(α) Πρέπεικαι
, από όπου προκύπτει ότι το πεδίο ορισμού της
είναι το
(β). (Δεν ξέρω αν η άσκηση ζητάει να βρούμε λύση με, ή χωρίς να είναι απαραίτητο να είναι
)
Ας βρούμε λύση για όλες τις δυνατές τιμές του πραγματικού αριθμού
Έχουμε, άρα
Τώρα η δοσμένη ανίσωση γράφεται:.
Θέτουμε, και έχουμε:
.
Οι ρίζες του τριωνύμου είναικαι δεδομένου ότι είναι και
, κατασκευάζοντας τον πίνακα,
βρίσκουμε ότικαι αφού
, παίρνουμε ότι
(ΣΗΜΕΙΩΣΗ: Αν θέλουμε να βρούμε λύσεις όταν, τότε έχουμε
)
(γ) Είναικαι
Αρχικά πρέπει
Τώρα η δοσμένη εξίσωση γράφεται:, (1)
Πρέπει επί πλέον να είναι, δηλαδή
και αφού είχαμε και
, τελικά θα
πρέπει.
Υψώνοντας τα μέλη της (1) στο τετράγωνο παίρνουμε την εξίσωση:, της οποίας η μόνη δεκτή ρίζα είναι η
.
(ΣΗΜΕΙΩΣΗ: Αν θέλουμε να βρούμε λύσεις όταν, δηλαδή όταν
, τότε πολύ πιο εύκολα, αφού είναι και
, έχουμε σαν μόνη πιθανή λύση την
, η οποία όμως δεν επαληθεύει την εξίσωση μας και άρα η εξίσωση
είναι αδύνατη.)
ήταν αρνητική. Αργότερα, (περίπου στις αρχές της δεκαετίας του 1980, θεωρήθηκε καλό από τους συγγραφείς του σχολικού
βιβλίου, να θεωρούμε όλα τα υπόριζα ως μη αρνητικά, για να μην μπερδεύονται οι μαθητές με τις παγίδες που υπήρχαν στις ιδιότητες
των ριζών. Έτσι έχει γίνει αυτή η σύμβαση στην χώρα μας (και σε μερικές ακόμα χώρες), ενώ υπάρχουν και άλλες χώρες, όπου δεν
έχουν υιοθετήσει αυτήν την σύμβαση.
Συνεπώς, δεν είναι λάθος μεν , αν θεωρήσουμε ότι ηέχει νόημα και όταν
, αλλά στα σχολικά δεδομένα
(στην Ελλάδα) θεωρούμε ότι έχει νόημα μόνο αν.
Venizelos έγραψε: ↑Τετ Δεκ 20, 2023 8:16 pmΝαι, δεν είναι κάτι το ασυνήθιστο μια τέτοια άσκηση για την Β Λυκείου.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Δεκ 20, 2023 8:13 pmΕυχαριστώ πολύ για τη διευκρίνιση! Αυτή ή άσκηση, θεωρείτε, θα μπορούσε να "πέσει" στις προαγωγικές της Β' Λυκείου ως κάποια υπερωτήματα;Venizelos έγραψε: ↑Τετ Δεκ 20, 2023 7:58 pmΠαλαιότερα, και στην Ελλάδα, τις κυβικές ρίζες (και γενικότερα οι περιττής τάξεως ρίζες), τις ορίζαμε και όταν η υπόριζη ποσότηταΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Δεκ 20, 2023 7:53 pmΠολύ σωστά. Είναι, όμως, απαραίτητο να πάρουμε περιορισμούς σε κυβική ρίζα; Ποια είναι η άποψή σας; Ρώτησα τον καθηγητή μου και μου είπε πως θα το ερευνήσει ο ίδιος.
ήταν αρνητική. Αργότερα, (περίπου στις αρχές της δεκαετίας του 1980, θεωρήθηκε καλό από τους συγγραφείς του σχολικού
βιβλίου, να θεωρούμε όλα τα υπόριζα ως μη αρνητικά, για να μην μπερδεύονται οι μαθητές με τις παγίδες που υπήρχαν στις ιδιότητες
των ριζών. Έτσι έχει γίνει αυτή η σύμβαση στην χώρα μας (και σε μερικές ακόμα χώρες), ενώ υπάρχουν και άλλες χώρες, όπου δεν
έχουν υιοθετήσει αυτήν την σύμβαση.
Συνεπώς, δεν είναι λάθος μεν , αν θεωρήσουμε ότι ηέχει νόημα και όταν
, αλλά στα σχολικά δεδομένα
(στην Ελλάδα) θεωρούμε ότι έχει νόημα μόνο αν.
Μόνο κατά την γνώμη μου, για να μην υπάρχει διχογνωμία από τους μαθητές, θα πρέπει να διευκρινίσουμε αν ζητάμε λύσεις μέσα στο
πεδίο ορισμού της συνάρτησης, ή λύσεις σε ένα ευρύτερο σύνολο στο οποίο ορίζεται η ανίσωση ή η εξίσωση.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες