 και
και  εφάπτονται εξωτερικά στο
εφάπτονται εξωτερικά στο  . Φέρω το εφαπτόμενο τμήμα
. Φέρω το εφαπτόμενο τμήμα 
και την ακτίνα
 . Τέλος , από το
. Τέλος , από το  φέρω το εφαπτόμενο τμήμα
φέρω το εφαπτόμενο τμήμα 
α) Δείξτε ότι :
 , συνευθειακά
, συνευθειακάβ) Υπολογίστε συναρτήσει των ακτίνων τα τμήματα :

γ) Ποιά η σχέση των ακτίνων αν :

Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 και
και  εφάπτονται εξωτερικά στο
εφάπτονται εξωτερικά στο  . Φέρω το εφαπτόμενο τμήμα
. Φέρω το εφαπτόμενο τμήμα 
 . Τέλος , από το
. Τέλος , από το  φέρω το εφαπτόμενο τμήμα
φέρω το εφαπτόμενο τμήμα 
 , συνευθειακά
, συνευθειακά

 , αφού
, αφού 
 από ισοσκελές τρίγωνο
από ισοσκελές τρίγωνο 
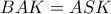 από ισοσκελές τρίγωνο
από ισοσκελές τρίγωνο 
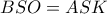 οπότε οι
οπότε οι  είναι αντικείμενες ημιευθείες, επομένως και τα σημεία
είναι αντικείμενες ημιευθείες, επομένως και τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. έχουμε:
έχουμε:  , άρα
, άρα 
 ως προς τον κύκλο
ως προς τον κύκλο 
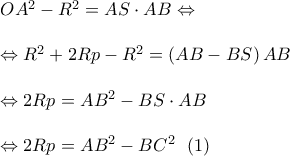
 (δύο γωνίες ίσες αντίστοιχα) παίρνουμε:
(δύο γωνίες ίσες αντίστοιχα) παίρνουμε:



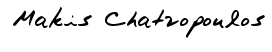
 το σημείο τομής των τμημάτων
το σημείο τομής των τμημάτων  και
και  , τότε αφού τα τρίγωνα
, τότε αφού τα τρίγωνα  και
και  είναι ισεμβαδικά έχουμε:
είναι ισεμβαδικά έχουμε:
 αφού και οι γωνίες
αφού και οι γωνίες  ως κατακορυφήν
ως κατακορυφήν άρα
άρα  , όμως και
, όμως και  (ως ακτίνα κάθετη στην εφαπτομένη), άρα η
(ως ακτίνα κάθετη στην εφαπτομένη), άρα η  διέρχεται από το κέντρο του κύκλου
διέρχεται από το κέντρο του κύκλου 
 (δες σημείωση) άρα εύκολα βρίσκουμε ότι:
(δες σημείωση) άρα εύκολα βρίσκουμε ότι: 
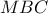 και έχουμε διαδοχικά:
και έχουμε διαδοχικά:
 ταυτίζεται με το σημείο
ταυτίζεται με το σημείο  , άρα δεν σχηματίζεται ορθογώνιο τρίγωνο, άρα δεν παίρνουμε Πυθαγόρειο Θεώρημα, αλλά κάνουμε τα εξής:
, άρα δεν σχηματίζεται ορθογώνιο τρίγωνο, άρα δεν παίρνουμε Πυθαγόρειο Θεώρημα, αλλά κάνουμε τα εξής: 
 τα ύψη των τριγώνων
τα ύψη των τριγώνων 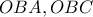 που αντιστοιχούν στην βάση
που αντιστοιχούν στην βάση 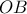 αντίστοιχα
αντίστοιχα διότι τα τρίγωνα
διότι τα τρίγωνα 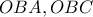 έχουν την ίδια βάση
έχουν την ίδια βάση 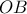
 ισαπέχουν από την ευθεία
ισαπέχουν από την ευθεία 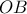 επομένως
επομένως 
 θα ισχύει
θα ισχύει 
 οπότε
οπότε  συνευθειακά δηλαδή
συνευθειακά δηλαδή 
 διότι
διότι  εφαπτόμενο τμήμα του κύκλου
εφαπτόμενο τμήμα του κύκλου  τότε
τότε 
 έχει
έχει  ορθές γωνίες τις
ορθές γωνίες τις  οπότε θα είναι ορθογώνιο
οπότε θα είναι ορθογώνιο  ως πλευρές ορθογωνίου
ως πλευρές ορθογωνίου  Αφού δεχόμαστε ότι ισχύει
Αφού δεχόμαστε ότι ισχύει  όπου
όπου 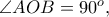 προκύπτει ότι
προκύπτει ότι  όπου
όπου  είναι η προβολή του
είναι η προβολή του  επί της ευθείας
επί της ευθείας 
 οφείλει να ανήκει στην ευθεία
οφείλει να ανήκει στην ευθεία 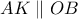
 από
από  και λόγω της
και λόγω της 
 αλλά και στον κύκλο
αλλά και στον κύκλο  συμπεραίνεται ότι
συμπεραίνεται ότι  και άρα το
και άρα το  ταυτίζεται με το αντιδιαμετρικό του
ταυτίζεται με το αντιδιαμετρικό του  στον κύκλο
στον κύκλο 
 έχει τρεις ορθές γωνίες
έχει τρεις ορθές γωνίες 
 , γιατί η
, γιατί η  είναι εφαπτομένη του
είναι εφαπτομένη του 
 και άρα έχουμε
και άρα έχουμε 
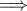
 .
. είναι ορθογώνιο παραλληλόγραμμο και από
είναι ορθογώνιο παραλληλόγραμμο και από 
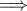
 και το (γ) ζητούμενο έχει βρεθεί.
και το (γ) ζητούμενο έχει βρεθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες