 και
και  του κύκλου
του κύκλου  τέμνονται κάθετα , και
τέμνονται κάθετα , και  είναι το μέσο της
είναι το μέσο της 
Η
 τέμνει τον κύκλο στο
τέμνει τον κύκλο στο  , και η
, και η 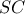 τη χορδή
τη χορδή  στο
στο  .
. Δείξτε ότι :
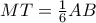 , και στη συνέχεια υπολογίστε το
, και στη συνέχεια υπολογίστε το 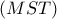 , ( συναρτήσει του
, ( συναρτήσει του  )
)Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 και
και  του κύκλου
του κύκλου  τέμνονται κάθετα , και
τέμνονται κάθετα , και  είναι το μέσο της
είναι το μέσο της 
 τέμνει τον κύκλο στο
τέμνει τον κύκλο στο  , και η
, και η 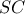 τη χορδή
τη χορδή  στο
στο  .
. 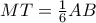 , και στη συνέχεια υπολογίστε το
, και στη συνέχεια υπολογίστε το 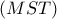 , ( συναρτήσει του
, ( συναρτήσει του  )
) έχουμε
έχουμε 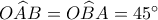 και
και 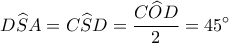 . Αν
. Αν  τότε το
τότε το 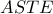 είναι εγγράψιμο και εφόσον
είναι εγγράψιμο και εφόσον 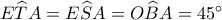 το τρίγωνο
το τρίγωνο  είναι ορθογώνιο και ισοσκελές και ισχύει
είναι ορθογώνιο και ισοσκελές και ισχύει  .
. 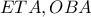 παίρνουμε:
παίρνουμε:  και από λόγο ομοιότητας των
και από λόγο ομοιότητας των 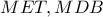 :
: 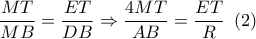 . Από
. Από  προκύπτει
προκύπτει  .
. 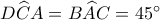 θα ισχύει
θα ισχύει 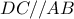 , οπότε τα τρίγωνα
, οπότε τα τρίγωνα 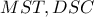 είναι όμοια, συνεπώς:
είναι όμοια, συνεπώς: ![\displaystyle\frac{{\left( {MST} \right)}}{{\left( {DSC} \right)}} = {\left( {\displaystyle\frac{{MT}}{{DC}}} \right)^2}\mathop = \limits^{\left[ {MT = \frac{{AB}}{6},DC = AB} \right]} \displaystyle\frac{1}{{36}}\,\,\left( 3 \right) \displaystyle\frac{{\left( {MST} \right)}}{{\left( {DSC} \right)}} = {\left( {\displaystyle\frac{{MT}}{{DC}}} \right)^2}\mathop = \limits^{\left[ {MT = \frac{{AB}}{6},DC = AB} \right]} \displaystyle\frac{1}{{36}}\,\,\left( 3 \right)](/forum/ext/geomar/texintegr/latexrender/pictures/87ca4b30b0d50a48fdca1233bf047b8b.png) .
. 
 . Από
. Από 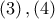
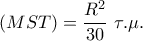
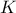 είναι το βαρύκεντρο του τριγώνου
είναι το βαρύκεντρο του τριγώνου 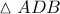 (
(  διάμεσοι) οπότε
διάμεσοι) οπότε  και
και 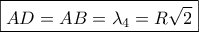
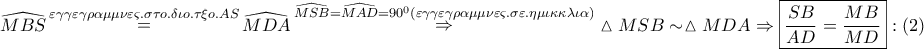

 (εγγεγραμμένες σε τεταρτοκύκλια) και
(εγγεγραμμένες σε τεταρτοκύκλια) και 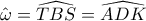 άρα
άρα 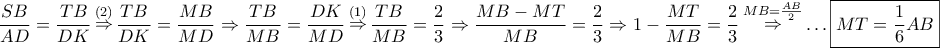
 και από την ομοιότητα
και από την ομοιότητα 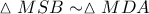 που είδαμε πιο πάνω με λόγο ομοιότητας από τη σχέση
που είδαμε πιο πάνω με λόγο ομοιότητας από τη σχέση 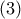
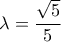 θα είναι
θα είναι 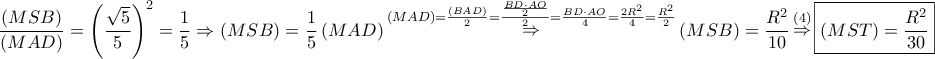 τ.μ.
τ.μ. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες