 , είναι "εγγεγραμμένο" σε τεταρτημόριο
, είναι "εγγεγραμμένο" σε τεταρτημόριο  , ακτίνας
, ακτίνας  .
. Ο κύκλος διαμέτρου
 , τέμνει το τετατροκύκλιο , στο σημείο
, τέμνει το τετατροκύκλιο , στο σημείο 
1) Δείξτε ότι η
 , είναι η διχοτόμος της γωνίας
, είναι η διχοτόμος της γωνίας 
2) Υπολογίστε το τμήμα
 , συναρτήσει του
, συναρτήσει του 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 , είναι "εγγεγραμμένο" σε τεταρτημόριο
, είναι "εγγεγραμμένο" σε τεταρτημόριο  , ακτίνας
, ακτίνας  .
.  , τέμνει το τετατροκύκλιο , στο σημείο
, τέμνει το τετατροκύκλιο , στο σημείο 
 , είναι η διχοτόμος της γωνίας
, είναι η διχοτόμος της γωνίας 
 , συναρτήσει του
, συναρτήσει του 
 όπου
όπου  είναι ο κύκλος διαμέτρου
είναι ο κύκλος διαμέτρου  (
(  το μέσο της
το μέσο της  ). Τότε επειδή
). Τότε επειδή  τετράγωνο θα είναι:
τετράγωνο θα είναι:  και το τετράπλευρο
και το τετράπλευρο  είναι ορθογώνιο
είναι ορθογώνιο  διάμετροι του κύκλου
διάμετροι του κύκλου  αφού
αφού  ) δηλαδή
) δηλαδή  .
. είναι η κοινή χορδή των κύκλων
είναι η κοινή χορδή των κύκλων  και συνεπώς θα είναι κάθετη στη διάκεντρό τους
και συνεπώς θα είναι κάθετη στη διάκεντρό τους  , δηλαδή
, δηλαδή  .
. (εγγεγραμμένη σε ημικύκλιο) οπότε και
(εγγεγραμμένη σε ημικύκλιο) οπότε και  . Από
. Από 
 ) και επειδή
) και επειδή  χορδές του
χορδές του  θα ισχύει:
θα ισχύει: 
 διχοτόμος της
διχοτόμος της 
 είναι ίση με
είναι ίση με  προφανώς η πλευρά του είναι
προφανώς η πλευρά του είναι 

 (επίκεντρη στον κύκλο
(επίκεντρη στον κύκλο  ) και
) και  .
.  είναι ισοσκελή (
είναι ισοσκελή (  και
και  ) και επειδή έχουν από την
) και επειδή έχουν από την  τις γωνίες των "κορυφών" τους
τις γωνίες των "κορυφών" τους . Τέλος στο ορθογώνιο τρίγωνο
. Τέλος στο ορθογώνιο τρίγωνο  από το Πυθαγόρειο Θεώρημα θα είναι:
από το Πυθαγόρειο Θεώρημα θα είναι: 
 :
:  και εφόσον
και εφόσον  (εγγεγραμμένη σε ημικύκλιο) θα είναι
(εγγεγραμμένη σε ημικύκλιο) θα είναι  .
.  (σχέση εγγεγραμμένης – επίκεντρης στο τεταρτοκύκλιο) και απ’ το ισοσκελές
(σχέση εγγεγραμμένης – επίκεντρης στο τεταρτοκύκλιο) και απ’ το ισοσκελές  θα είναι
θα είναι  .
. θα είναι
θα είναι  , απ’ το τρίγωνο
, απ’ το τρίγωνο  :
:  και το ζητούμενο αποδείχτηκε.
και το ζητούμενο αποδείχτηκε. με
με  και
και  παίρνουμε
παίρνουμε  . Από Πυθαγόρειο στο
. Από Πυθαγόρειο στο  παίρνουμε
παίρνουμε  , οπότε
, οπότε  .
. και
και  . Το
. Το  είναι μέσο του
είναι μέσο του 
 , άρα στο τρίγωνο
, άρα στο τρίγωνο  :
:  .
. 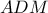 (
( ) παίρνουμε
) παίρνουμε  . Τα τρίγωνα
. Τα τρίγωνα  είναι όμοια, συνεπώς
είναι όμοια, συνεπώς  .
.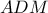 με Π.Θ. βρίσκουμε
με Π.Θ. βρίσκουμε  . Αλλά το
. Αλλά το  είναι όμοιο με το
είναι όμοιο με το 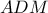
 , απ΄όπου παίρνω :
, απ΄όπου παίρνω : 

 παίρνουμε τα σημεία
παίρνουμε τα σημεία  . Με κέντρο το
. Με κέντρο το  και ακτίνα
και ακτίνα  κατασκευάζουμε τεταρτοκύκλιο
κατασκευάζουμε τεταρτοκύκλιο  , όπου
, όπου  , με εξίσωση:
, με εξίσωση: 
 του
του  έχει συντεταγμένες
έχει συντεταγμένες  . Είναι
. Είναι 
 έχει εξίσωση:
έχει εξίσωση: 
 που είναι ρίζες του συστήματος των εξισώσεων τους.
που είναι ρίζες του συστήματος των εξισώσεων τους. , οπότε, εκτός από το
, οπότε, εκτός από το  τέμνονται και στο
τέμνονται και στο 

 και αφού είναι και οι δύο οξείες (το
και αφού είναι και οι δύο οξείες (το  είναι ορθογώνιο με
είναι ορθογώνιο με  ), είναι ίσες.
), είναι ίσες.
 είναι
είναι 
 είναι απλά ορθογώνιο και όχι κατ’ αν’ ανάγκη τετράγωνο, ως εξής:
είναι απλά ορθογώνιο και όχι κατ’ αν’ ανάγκη τετράγωνο, ως εξής: περνά από τα σημεία
περνά από τα σημεία  Έστω
Έστω  το σημείο τομής της
το σημείο τομής της  με τον κύκλο αυτό, τότε ισχύει
με τον κύκλο αυτό, τότε ισχύει 
 είναι ορθογώνιο, οπότε
είναι ορθογώνιο, οπότε 
 , το
, το  είναι εγγράψιμο και
είναι εγγράψιμο και  που σημαίνει
που σημαίνει  .
. είναι διχοτόμος της
είναι διχοτόμος της  .
. , συμμετρικό του
, συμμετρικό του  ως προς το κέντρο
ως προς το κέντρο  . Τότε
. Τότε  (βαίνει σε ημικύκλιο ) αλλά και
(βαίνει σε ημικύκλιο ) αλλά και  (αφού
(αφού 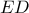 διάμετρος ).
διάμετρος ). είναι συνευθειακά.
είναι συνευθειακά. παίρνουμε
παίρνουμε  και
και  .
.  προφανώς είναι σημείο της μεσοκαθέτου του
προφανώς είναι σημείο της μεσοκαθέτου του  άρα
άρα  ..
..Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 4 επισκέπτες