 τα σημεία
τα σημεία  είναι μέσα των πλευρών
είναι μέσα των πλευρών  , αντίστοιχα, και
, αντίστοιχα, και  το ύψος από το
το ύψος από το  . Ο κύκλος που περνά από τα
. Ο κύκλος που περνά από τα 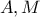 και εφάπτεται στην
και εφάπτεται στην  , τέμνει την
, τέμνει την  στο
στο  .
.Να βρείτε την ελάχιστη τιμή του λόγου
 , κάθως και για ποια τρίγωνα
, κάθως και για ποια τρίγωνα  επιτυγχάνεται η ελάχιστη τιμή .
επιτυγχάνεται η ελάχιστη τιμή .Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 τα σημεία
τα σημεία  είναι μέσα των πλευρών
είναι μέσα των πλευρών  , αντίστοιχα, και
, αντίστοιχα, και  το ύψος από το
το ύψος από το  . Ο κύκλος που περνά από τα
. Ο κύκλος που περνά από τα 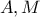 και εφάπτεται στην
και εφάπτεται στην  , τέμνει την
, τέμνει την  στο
στο  .
. , κάθως και για ποια τρίγωνα
, κάθως και για ποια τρίγωνα  επιτυγχάνεται η ελάχιστη τιμή .
επιτυγχάνεται η ελάχιστη τιμή .Είναι κρίμα ''να μείνει στο ράφι''...Ορέστης Λιγνός έγραψε:Σε τρίγωνοτα σημεία
είναι μέσα των πλευρών
, αντίστοιχα, και
το ύψος από το
. Ο κύκλος που περνά από τα
και εφάπτεται στην
, τέμνει την
στο
.
Να βρείτε την ελάχιστη τιμή του λόγου, κάθως και για ποια τρίγωνα
επιτυγχάνεται η ελάχιστη τιμή .
Καλησπέρα,Ορέστης Λιγνός έγραψε:Σε τρίγωνοτα σημεία
είναι μέσα των πλευρών
, αντίστοιχα, και
το ύψος από το
. Ο κύκλος που περνά από τα
και εφάπτεται στην
, τέμνει την
στο
.
Να βρείτε την ελάχιστη τιμή του λόγου, κάθως και για ποια τρίγωνα
επιτυγχάνεται η ελάχιστη τιμή .
LOGOS.png
 οπότε
οπότε  (1)
(1) και
και  είναι όμοια, αφού
είναι όμοια, αφού  λόγο χορδής και εφαπτομένης και
λόγο χορδής και εφαπτομένης και  ως εντός εναλλάξ. Οπότε θα ισχύει
ως εντός εναλλάξ. Οπότε θα ισχύει  . H (1) τώρα γράφεται
. H (1) τώρα γράφεται

 .
. είναι ορθογώνιο στο
είναι ορθογώνιο στο  και
και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης