 κινείται στον έγκυκλο ισοπλεύρου τριγώνου
κινείται στον έγκυκλο ισοπλεύρου τριγώνου  πλευράς
πλευράς  Να βρείτε την ελάχιστη τιμή
Να βρείτε την ελάχιστη τιμή του αθροίσματος
 και να εντοπίσετε το σημείο
και να εντοπίσετε το σημείο 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 κινείται στον έγκυκλο ισοπλεύρου τριγώνου
κινείται στον έγκυκλο ισοπλεύρου τριγώνου  πλευράς
πλευράς  Να βρείτε την ελάχιστη τιμή
Να βρείτε την ελάχιστη τιμή  και να εντοπίσετε το σημείο
και να εντοπίσετε το σημείο 
 . Έστω
. Έστω  η πλευρά του περιγεγραμμένου τριγώνου και
η πλευρά του περιγεγραμμένου τριγώνου και  το ύψος του.
το ύψος του. , οπότε
, οπότε  .
. .
.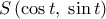 σημείο του κύκλου, με
σημείο του κύκλου, με  .
.

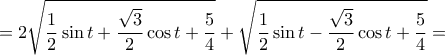
 .
. περίπου ίσο με
περίπου ίσο με  και ελάχιστη τιμή
και ελάχιστη τιμή  , με πλευρά τριγώνου
, με πλευρά τριγώνου  , άρα ανάγοντάς το σε τυχαία πλευρά
, άρα ανάγοντάς το σε τυχαία πλευρά  , είναι
, είναι  .
.
 και
και  τα μέσα των πλευρών
τα μέσα των πλευρών 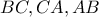 .
. του
του  και
και  του
του  .
. διαγράφει το κύκλο
διαγράφει το κύκλο  και η
και η 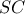 τέμνει τον κύκλο
τέμνει τον κύκλο  στο σημείο
στο σημείο  .
. το μέσο του
το μέσο του 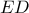 τότε το
τότε το  είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  .
. . Το λογιστικό μετά μέρος εύκολο.
. Το λογιστικό μετά μέρος εύκολο. . Έστω
. Έστω  το μέσον του
το μέσον του  .
. τα
τα  μέσα , άρα
μέσα , άρα  δηλ το
δηλ το  ανήκει στον μικρό κύκλο
ανήκει στον μικρό κύκλο 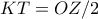 ).
).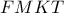 είναι χαρταετός αφού
είναι χαρταετός αφού 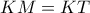 και
και 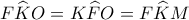 . Άρα
. Άρα  .
. 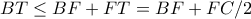 ,
,  είναι η τομή του
είναι η τομή του  με τον έγκυκλο του
με τον έγκυκλο του 
 (με Πυθαγόρειο στο ορθ.
(με Πυθαγόρειο στο ορθ.  )..
)..Λίγο διαφορετικά από το αγαπητό Γιώργο Μήτσιο στην απόδειξή του λήμματος.george visvikis έγραψε:Ελάχιστο αθροίσματος.png
Το σημείοκινείται στον έγκυκλο ισοπλεύρου τριγώνου
πλευράς
Να βρείτε την ελάχιστη τιμή
του αθροίσματοςκαι να εντοπίσετε το σημείο
 είναι βαρύκεντρο του
είναι βαρύκεντρο του  ,το δε
,το δε  μέσο του
μέσο του  , ισχύει:
, ισχύει:  . Δηλαδή η δέσμη
. Δηλαδή η δέσμη  είναι αρμονική και αφού
είναι αρμονική και αφού  γιατί βαίνει σε ημικύκλιο στο τρίγωνο
γιατί βαίνει σε ημικύκλιο στο τρίγωνο  η
η  είναι εσωτερική
είναι εσωτερική  είναι το εξωτερικό κέντρο ομοιότητας των δύο κύκλων ,
είναι το εξωτερικό κέντρο ομοιότητας των δύο κύκλων ,  . Μετά απ’ αυτά :
. Μετά απ’ αυτά :  , άρα το
, άρα το  είναι ισοσκελές
είναι ισοσκελές  είναι μέσο του
είναι μέσο του 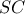 .
. έχω:
έχω: 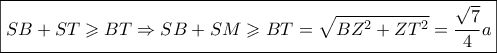 .
. (στο σχήμα του Νίκου) που φαίνεται να είναι
(στο σχήμα του Νίκου) που φαίνεται να είναι  (αλλά δεν έχω απόδειξη και μπορεί να κάνω και λάθος).Να πω όμως δυο λόγια για το γεωμετρικό αυτό πρόβλημα.
(αλλά δεν έχω απόδειξη και μπορεί να κάνω και λάθος).Να πω όμως δυο λόγια για το γεωμετρικό αυτό πρόβλημα. του έγκυκλου είναι
του έγκυκλου είναι  (
( μέσο του
μέσο του  ) Άρα:
) Άρα: , που λύνει κατασκευαστικά το πρόβλημα και απλουστεύει τον υπολογισμό.
, που λύνει κατασκευαστικά το πρόβλημα και απλουστεύει τον υπολογισμό. και τότε η
και τότε η  , που αναφέρει ο Γιώργος πριν
, που αναφέρει ο Γιώργος πριν  ..το μόνο που κατάφερα να ''δείξω'' με χρήση της τεχνολογίας είναι ότι η γωνία αυτή ΔΕΝ είναι ακριβώς
..το μόνο που κατάφερα να ''δείξω'' με χρήση της τεχνολογίας είναι ότι η γωνία αυτή ΔΕΝ είναι ακριβώς  ..
..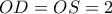 τότε είναι
τότε είναι  . Ακόμη είναι
. Ακόμη είναι  και θέτω
και θέτω  οπότε
οπότε  .
. προκύπτουν
προκύπτουν  άρα
άρα .
.  για να έχουμε μέγιστο , το μετατρέπουμε από ακτίνια σε μοίρες και παίρνουμε
για να έχουμε μέγιστο , το μετατρέπουμε από ακτίνια σε μοίρες και παίρνουμε  . Στη συνέχεια εντοπίζουμε το
. Στη συνέχεια εντοπίζουμε το  και μετράει για χάρη μας
και μετράει για χάρη μας 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες