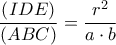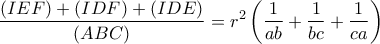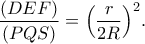Κατ' αρχήν να ευχαριστήσω θερμά το Γιώργο Βισβίκη για τη λύση του.
Ας δούμε το πώς έφτασα στο θέμα αυτό...
Σε παλιά βιβλία γεωμετρίας συναντάμε ως άλυτη άσκηση το εξής:
Έστω τρίγωνο 
Aν  το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου του
το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου του  με τις πλευρές του.
με τις πλευρές του.
Αποδείξτε ότι

Aς δώσω μια λύση...
Έστω

το έγκεντρο του τριγώνου

Αυτό που αμέσως βλέπει κάποιος , λόγω του εγγραψίμου τετραπλεύρου

, είναι

Αυτό όμως συνεπάγεται ότι

και έτσι

και μπορώ πλέον να γράψω ότι

Για να μην κουράζω , μπορώ να γράψω ότι ισχύει αντίστοιχα

και
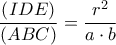
Έτσι τώρα πια μπορώ να γράψω ότι

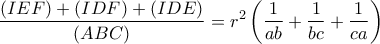
Όμως

και βέβαια ισχύει

Συνεπώς μπορεί να γραφεί ότι ισχύει

Από εδώ και πέρα για να διατυπώσω το προτεινόμενο θέμα σκέφτηκα ως εξής:
Από
εδώ είναι
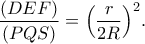
Μπορώ πλέον να γράψω ότι

Η ισότητα που ζητάμε είναι πλέον προφανής.
Σχήμα δεν κάνω , νομίζω ότι αυτό που σχεδίασε ο Γιώργος Βισβίκης είναι αρκετό...
Κοιτάτε τα παλιά βιβλία , δίνουν ωραίες ιδέες...

 το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου του
το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου του  με τις πλευρές του. Έστω επίσης
με τις πλευρές του. Έστω επίσης  τα παράκεντρα του
τα παράκεντρα του 
 είναι μέσο ανάλογο των εμβαδών των τριγώνων
είναι μέσο ανάλογο των εμβαδών των τριγώνων  και
και 

 με
με 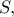 επειδή χρησιμοποιώ το
επειδή χρησιμοποιώ το  όπως επίσης την ακτίνα
όπως επίσης την ακτίνα 
 των παρεγγεγραμμένων κύκλων και
των παρεγγεγραμμένων κύκλων και  την ημιπερίμετρο.
την ημιπερίμετρο.  Αρκεί να δείξω λοιπόν ότι:
Αρκεί να δείξω λοιπόν ότι: 



 και το ζητούμενο έπεται.
και το ζητούμενο έπεται.
 οι προβολές των
οι προβολές των  πάνω στη
πάνω στη 
 το μέσο του
το μέσο του  και
και  η διάμετρος του κύκλου
η διάμετρος του κύκλου 
 Το τμήμα
Το τμήμα  είναι η διάμεσος του τραπεζίου
είναι η διάμεσος του τραπεζίου  οπότε
οπότε 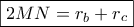

 ενώνει τα μέσα των διαγωνίων του τραπεζίου
ενώνει τα μέσα των διαγωνίων του τραπεζίου  άρα
άρα 



 το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου του
το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου του 
 το έγκεντρο του τριγώνου
το έγκεντρο του τριγώνου  , είναι
, είναι 
 και έτσι
και έτσι