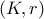 εφάπτεται σε ημικύκλιο διαμέτρου
εφάπτεται σε ημικύκλιο διαμέτρου  σε σημείο
σε σημείο  και στη διάμετρο του ημικυκλίου
και στη διάμετρο του ημικυκλίου σε κάποιο σημείο της. Αν
 να βρείτε το λόγο
να βρείτε το λόγο  συναρτήσει της
συναρτήσει της 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
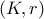 εφάπτεται σε ημικύκλιο διαμέτρου
εφάπτεται σε ημικύκλιο διαμέτρου  σε σημείο
σε σημείο  και στη διάμετρο του ημικυκλίου
και στη διάμετρο του ημικυκλίου  να βρείτε το λόγο
να βρείτε το λόγο  συναρτήσει της
συναρτήσει της 

 η προβολή του
η προβολή του  στη διάμετρο
στη διάμετρο  . Φέρνω την εφαπτομένη του
. Φέρνω την εφαπτομένη του  που τέμνει τη ευθεία
που τέμνει τη ευθεία  στο
στο  .
. έχω :
έχω : 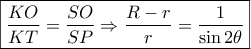


 Από κατασκευής του κύκλου η
Από κατασκευής του κύκλου η  διέρχεται από το νότιο πόλο του
διέρχεται από το νότιο πόλο του 
 και
και


 όπου δίνει
όπου δίνει 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες