 , του παραπάνω σχήματος, δίνονται:
, του παραπάνω σχήματος, δίνονται:  και
και  . Να βρείτε το μήκος του τμήματος
. Να βρείτε το μήκος του τμήματος 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 , του παραπάνω σχήματος, δίνονται:
, του παραπάνω σχήματος, δίνονται:  και
και  . Να βρείτε το μήκος του τμήματος
. Να βρείτε το μήκος του τμήματος 

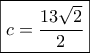
 και
και  είναι
είναι  και άρα η γωνία
και άρα η γωνία  ισούται με
ισούται με 
 κάθετη στην
κάθετη στην και αφού είναι
και αφού είναι  και
και  , άρα
, άρα 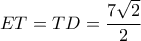
 και
και  .
. και
και  έχουμε:
έχουμε:  και άρα
και άρα , (ΣΧΕΣΗ 1)
, (ΣΧΕΣΗ 1) παίρνουμε:
παίρνουμε: , (ΣΧΕΣΗ 2)
, (ΣΧΕΣΗ 2) έχουμε:
έχουμε: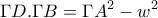 και άρα λόγω και των σχέσεων 1 και 2 έχουμε:
και άρα λόγω και των σχέσεων 1 και 2 έχουμε:
 και έστω
και έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  . Επειδή η
. Επειδή η 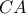 είναι μεσοκάθετος στο
είναι μεσοκάθετος στο  αβίαστα προκύπτουν τα παρακάτω:
αβίαστα προκύπτουν τα παρακάτω: 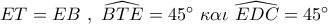 .
.  είναι έγκεντρο του
είναι έγκεντρο του  και έστω
και έστω 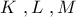 τα σημεία επαφής του εγγεγραμμένου κύκλου με τις
τα σημεία επαφής του εγγεγραμμένου κύκλου με τις  αντίστοιχα .
αντίστοιχα . .
.  είναι :
είναι :  (1)
(1) ενώ
ενώ  Μα έτσι
Μα έτσι  .
.  ,
,  θα έχω :
θα έχω : ή
ή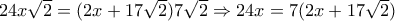 και άρα
και άρα 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες