Η

είναι η εξωτερική διχοτόμος της γωνίας

του

, οπότε

.
Για να αποδείξουμε ότι η

εφάπτεται του κύκλου

, αρκεί

, που προκύπτει
άμεσα όταν το τετράπλευρο

είναι εγγράψιμο. Γι' αυτό αρκεί

, όπου

το σημείο τομής των ευθειών

και

.
Αποδεικνύεται ότι το

είναι το σημείο επαφής της πλευράς

με τον
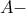
παρεγγεγραμμένο
κύκλο του

. Επομένως,

(βλέπε το Λήμμα 1 στη
viewtopic.php?f=22&t=68626.

- Tang_to_inc.png (51.31 KiB) Προβλήθηκε 793 φορές
Επίσης έχουμε

(Η απόδειξη στο τέλος

). Εφόσον τα ορθογώνια τρίγωνα

και

έχουν τις οξείες γωνίες τους

και

ίσες, τότε και οι άλλες οξείες γωνίες τους
θα είναι ίσες, δηλαδή,

.
Από

και


που σημαίνει ότι το

είναι εγγράψιμο.

Θεωρούμε τον περιγεγραμμένο κύκλο του τριγώνου

, και έστω

,

τα σημεία τομής του
με τις πλευρές

και

του τριγώνου

αντίστοιχα. Τότε έχουμε

(Λήμμα 2)
και

(Λήμμα 3) οπότε

.
Επομένως τα σημεία

και

είναι συμμετρικά ως προς τη διχοτόμο

. Ως εκ τούτου

.
Δίνουμε τις διατυπώσεις των δύο λημμάτων που χρησιμοποιήθηκαν χωρίς τις αποδείξεις τους, που άλλωστε δεν παρουσιάζουν δυσκολία.
Λήμμα 2.
Στις πλευρές  και
και  ενός σκαληνού τριγώνου
ενός σκαληνού τριγώνου  ,
,  , θεωρούμε αντίστοιχα τα σημεία
, θεωρούμε αντίστοιχα τα σημεία  και
και  .
.
Το σημείο  είναι το μέσο του τόξου
είναι το μέσο του τόξου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  . Να αποδείξετε ότι
. Να αποδείξετε ότι
η ισότητα  ισχύει, αν και μόνο αν, τα σημεία
ισχύει, αν και μόνο αν, τα σημεία  ,
,  ,
,  ,
,  είναι ομοκυκλικά.
είναι ομοκυκλικά.
Λήμμα 3.
Στις πλευρές  και
και  ενός σκαληνού τριγώνου
ενός σκαληνού τριγώνου  ,
,  , θεωρούμε αντίστοιχα τα σημεία
, θεωρούμε αντίστοιχα τα σημεία  και
και  ,
,
το σημείο  είναι το κέντρο του εγγεγραμμένου στο τρίγωνο
είναι το κέντρο του εγγεγραμμένου στο τρίγωνο  κύκλου. Να αποδείξετε ότι ο περιγεγραμμένος κύκλος
κύκλου. Να αποδείξετε ότι ο περιγεγραμμένος κύκλος
του τριγώνου  , διέρχεται από το σημείο
, διέρχεται από το σημείο  αν και μόνο αν
αν και μόνο αν  .
. και
και  είναι αντίστοιχα ο περιγεγραμμένος και ο εγγεγραμμένος ενός σκαληνού τριγώνου
είναι αντίστοιχα ο περιγεγραμμένος και ο εγγεγραμμένος ενός σκαληνού τριγώνου  . Συμβολίζουμε με
. Συμβολίζουμε με  το μέσο του τόξου
το μέσο του τόξου  τού κύκλου
τού κύκλου  , με
, με  το έγκεντρο του
το έγκεντρο του  , με
, με  το σημείο επαφής του
το σημείο επαφής του  με την πλευρά
με την πλευρά  , με
, με 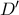 το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον
στον , και με
, και με  το σημείο τομής της ευθείας
το σημείο τομής της ευθείας  με την κάθετο της
με την κάθετο της  στο
στο  .
.  εφάπτεται του
εφάπτεται του  .
.



 και η εφαπτομένη στο
και η εφαπτομένη στο  .
. τέμνει τον κύκλο διαμέτρου
τέμνει τον κύκλο διαμέτρου  .
. ή ισοδύναμα
ή ισοδύναμα 
 μέσον την
μέσον την  το αντιδιαμετρικό του
το αντιδιαμετρικό του  προς τον
προς τον  και
και  η τομή του κύκλου Euler του
η τομή του κύκλου Euler του  όπου
όπου  το περίκεντρο του
το περίκεντρο του 
 οπότε η
οπότε η  περνά από το αντιδιαμετρικό
περνά από το αντιδιαμετρικό  του
του  όπου
όπου  το ορθόκεντρο.
το ορθόκεντρο. συνευθειακά οπότε είναι πλέον απλό ότι
συνευθειακά οπότε είναι πλέον απλό ότι  και τελειώσαμε.
και τελειώσαμε. , οπότε
, οπότε  .
. , που προκύπτει
, που προκύπτει είναι εγγράψιμο. Γι' αυτό αρκεί
είναι εγγράψιμο. Γι' αυτό αρκεί  , όπου
, όπου 
 και
και 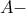 παρεγγεγραμμένο
παρεγγεγραμμένο  (βλέπε το Λήμμα 1 στη
(βλέπε το Λήμμα 1 στη  (Η απόδειξη στο τέλος
(Η απόδειξη στο τέλος  ). Εφόσον τα ορθογώνια τρίγωνα
). Εφόσον τα ορθογώνια τρίγωνα  και
και  έχουν τις οξείες γωνίες τους
έχουν τις οξείες γωνίες τους  και
και  ίσες, τότε και οι άλλες οξείες γωνίες τους
ίσες, τότε και οι άλλες οξείες γωνίες τους  .
. και
και 
 που σημαίνει ότι το
που σημαίνει ότι το  είναι εγγράψιμο.
είναι εγγράψιμο. , και έστω
, και έστω  ,
,  τα σημεία τομής του
τα σημεία τομής του  και
και  του τριγώνου
του τριγώνου  (Λήμμα 2)
(Λήμμα 2)  (Λήμμα 3) οπότε
(Λήμμα 3) οπότε  .
. είναι συμμετρικά ως προς τη διχοτόμο
είναι συμμετρικά ως προς τη διχοτόμο  . Ως εκ τούτου
. Ως εκ τούτου  .
. , θεωρούμε αντίστοιχα τα σημεία
, θεωρούμε αντίστοιχα τα σημεία  και
και  .
.  είναι το μέσο του τόξου
είναι το μέσο του τόξου  ισχύει, αν και μόνο αν, τα σημεία
ισχύει, αν και μόνο αν, τα σημεία  , θεωρούμε αντίστοιχα τα σημεία
, θεωρούμε αντίστοιχα τα σημεία  , διέρχεται από το σημείο
, διέρχεται από το σημείο  .
. οπότε
οπότε 
![\cos \angle PID{'}=\sin \angle A_{1}ID=\sin \left [ 180^\circ+\frac{A}{2} -\left ( 180^\circ -B-u\right ) \right ]=\sin \left ( \frac{A}{2}+B+u \right ). \cos \angle PID{'}=\sin \angle A_{1}ID=\sin \left [ 180^\circ+\frac{A}{2} -\left ( 180^\circ -B-u\right ) \right ]=\sin \left ( \frac{A}{2}+B+u \right ).](/forum/ext/geomar/texintegr/latexrender/pictures/5a770893dfa1c50588adfcfda5de0ee1.png)
 αρκεί ν.δ.ο
αρκεί ν.δ.ο 

 αρκεί ν.δ.ο
αρκεί ν.δ.ο  που είναι άμεση από το ανάπτυγμα
που είναι άμεση από το ανάπτυγμα  .
.