Στήν άσκηση πέντε β' όμαδας στο εσωτερικό γινόμενο στο σχολικό βιβλίο λέει
αν τα διανύσματα
 καί
καί  είναι κάθετα καί έχουν μέτρα ίσα με την μονάδα να αποδείξετε ότι
είναι κάθετα καί έχουν μέτρα ίσα με την μονάδα να αποδείξετε ότι  .
. Ενας τρόπος λύσης είναι να θεωρήσουμε την ταυτότητα
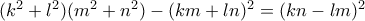 .
.Υπάρχει κάποιος άλλος τρόπος πιο ας πούμε πιό ''κομψός" ?





 και
και  με κοινή αρχή την αρχή των αξόνων.
με κοινή αρχή την αρχή των αξόνων. 





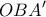 η
η  είναι διχοτόμος κι επειδή είναι ισοσκελές(
είναι διχοτόμος κι επειδή είναι ισοσκελές( )
)


![\displaystyle{
\omega ,\theta \in [0,2\pi ]
} \displaystyle{
\omega ,\theta \in [0,2\pi ]
}](/forum/ext/geomar/texintegr/latexrender/pictures/8e09106b0d6e0c1d05f42413b301505f.png)






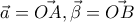 με κοινή αρχή το Ο, οπότε το εμβαδόν του τριγώνου
με κοινή αρχή το Ο, οπότε το εμβαδόν του τριγώνου  , υπολογιζόμενο με δύο τρόπους δίνει:
, υπολογιζόμενο με δύο τρόπους δίνει:

