Κωνική τομή : Γιατί είναι έλλειψη ;

#1

Το παρακάτω σχήμα δείχνει πρακτικά την τομή κώνου με επίπεδο.Οι εστίες βρίσκονται στα ...καρφάκια.

Μαζί με τα άλλα αντίστοιχα σχήματα, οι σφαίρες του Dandelin αποτελούν μια αξιοθαύμαστη γεωμετρική επινόηση .

: dandelin spheres.PNG (44.08 KiB) Προβλήθηκε 1810 φορές

Στα παρακάτω σχήματα ο κώνος φαίνεται πιο γεωμετρικά :

: 2014-4-28, dandelin.PNG (229.53 KiB) Προβλήθηκε 1810 φορές

#2

Μπάμπης Στεργίου έγραψε:Το παρακάτω σχήμα δείχνει πρακτικά την τομή κώνου με επίπεδο.Οι εστίες βρίσκονται στα ...καρφάκια.

Μπάμπη καλημέρα και Χρόνια Πολλά.

Τα ωραία σχήματά σου με προκάλεσαν να πάω το θέμα λίγο πιο πέρα αναφερόμενος

στα ακόλουθα σχήματα που κατασκεύασα με το λογισμικό Cabri3d.

: Έλλειψη - Κωνική τομή 2.PNG (242.5 KiB) Προβλήθηκε 1720 φορές

Στο ανωτέρω σχήμα έγινε πλάγια τομή της επιφάνειας μιας ορθής κυκλικής κωνικής επιφάνειας

η οποία είναι η έλλειψη(πράσινο χρώμα) με μεγάλο άξονα τον $\displaystyle{CD}$ .

Επίσης έχουν κατασκευαστεί οι δύο σφαίρες που εφάπτονται της ανωτέρω κωνικής επιφάνειας

καθώς επίσης και του τέμοντος επιπέδου στα σημεία $\displaystyle{E_1, E_2}$ .

(Οι σφαίρες αυτές είναι η εγγεγραμμένη και η παρεγγεγραμμένη στον κώνο $\displaystyle{(O.CD)}$ )

Στο επόμενο σχήμα κρύβω την κωνική επιφάνεια για να φανεί καλύτερα το περιεχόμενο.

: Έλλειψη - Κωνική τομή 1.PNG (151.78 KiB) Προβλήθηκε 1720 φορές

Στο σχήμα αυτό θα δείξουμε ότι οι αποστάσεις ενός τυχαίου σημείου $\displaystyle{M}$ της έλλειψης

από τα σημεία επαφής των σφαιρών με το επίπεδο τομής, δηλαδή από τα σημεία $\displaystyle{E_1,E_2}$

είναι σταθερό.

Θα δείξουμε δηλαδή ότι για κάθε $\displaystyle{M}$ της ελλειψης ισχύει:

$\displaystyle{ME_1+ME_2=ct}$

Πράγματι είναι:

$\displaystyle{ME_1=MA\ \ (1) }$ και $\displaystyle{ME_2=MB \ \ (2) }$

όπου $\displaystyle{AB}$ η κοινή εξωτερική εφαπτομένη των σφαιρών που διέρχεται φυσικά από το σημείο $\displaystyle{O}$ .

(Θυμίζουμε ότι οι εφαπτόμενες που άγονται από ένα εξωτερικό σημείο μιας σφαίρας προς

τη σφαίρα αυτή είναι ίσες).

Προσθέτοντας τις (1) και (2) προκύπτει:

$\displaystyle{ME_1+ME_2=MA+MB=AB=ct}$

διότι το μήκος της κοινής αυτής εξωτερικής εφαπτομένης είναι σταθερό για κάθε θέση

του σημείου $\displaystyle{M}$ που διατρέχει την έλλειψη αυτή.

Σχόλια:

1. Όπως φαίνεται η ιδιότητα αυτή είναι απόρροια του ορισμού της κωνινής τομής κι όχι πρωτογενής ορισμός όπως διδάσκεται στη Β' Λυκείου

κι αυτό βέβαια γίνεται για διδακτικούς λόγους.

2. Το ίδιο μπορούμε να κάνουμε και για τις άλλες κωνικές τομές.

Κώστας Δόρτσιος

#3

Κώστα, υπέροχα πράγματα !

Νάσαι καλά !

Christos.N · #4

Μου έχει δημιουργηθεί η απορία πως εγγράφουμε τις δύο σφαίρες που εφάπτονται του επιπέδου και του κώνου.

Υ.Γ. Συγκεκριμένα έχω απορία πως θα βρούμε τον μεγάλο άξονα της έλλειψης.

Christos.N · #5

Η απορία μου όμως είχε απαντηθεί ήδη εδώ

#6

Christos.N έγραψε: ↑
Τετ Φεβ 21, 2018 12:10 am
Μου έχει δημιουργηθεί η απορία πως εγγράφουμε τις δύο σφαίρες που εφάπτονται του επιπέδου και του κώνου.

Υ.Γ. Συγκεκριμένα έχω απορία πως θα βρούμε τον μεγάλο άξονα της έλλειψης.

Χρήστο καλησπέρα από Γρεβενά...

Για την απορία που διατυπώνεις, δηλαδή για την εγγραφή των σφαιρών σε κωνική επιφάνεια καθώς
και το πώς βρίσκουμε τον μεγάλο άξονα της έλλειψης που προκύπτει από την τομή δοθείσης
κωνικής επιφάνειας με δοθέν επίπεδο, προσπάθησα, μιας και παλιότερα είχα αναρτήσει τα
παραπάνω σχήματα, και με μερικά ακόμα σχήματα να διατυπώσω μια άποψη.

Για να φτάσουμε στην απάντησή στο ερώτημά σου προτάσω αρχικά το εξής:

-"Να κατασκευαστεί (εννοείται με κανόνα και διαβήτη) η κάθετη που άγεται από δοθέν σημείο $\displaystyle{A}$
προς ένα επίπεδο $\displaystyle{(p)}$ "
Στο πρώτο σχήμα δίνεται το σημείο $\displaystyle{A}$ (έστω εκτός του επιπέδου (p)) και ζητούμε να φέρουμε την κάθετη
$\displaystyle{AB}$ προς το επίπεδο $\displaystyle{(p)}$ .

: Κάθετη από δοθέν σημείο προς ένα επίπεδο 1.png (8.56 KiB) Προβλήθηκε 1180 φορές

Κατασκευή:
Εργαζόμαστε στο δεύτερο σχήμα:

: Κάθετη από δοθέν σημείο προς ένα επίπεδο 2.png (77.74 KiB) Προβλήθηκε 1180 φορές

Στο δοθέν επίπεδο $\displaystyle{(p)}$ θεωρούμε τυχαία ευθεία $\displaystyle{(e)}$ . Στο επίπεδο $\displaystyle{(q)}$ που ορίζει το σημείο $\displaystyle{A}$ και
η ευθεία $\displaystyle{(e)}$ μπορούμε με κανόνα και διαβήτη να φέρουμε την κάθετη από το σημείο $\displaystyle{A}$ προς την $\displaystyle{(e)}$
δηλαδή την $\displaystyle{AC}$ κατά τα γνωστά.

Στο επίπεδο τώρα $\displaystyle{(p)}$ μπορούμε να φέρουμε την κάθετη επί της $\displaystyle{(e)}$ στο σημείο αυτής $\displaystyle{C}$ , δηλαδή
την $\displaystyle{Ce_1}$ πάλι κατά τα γνωστά με κανόνα και διαβήτη.

Τέλος στο επίπεδο $\displaystyle{(r)}$ που ορίζεται από το σημείο $\displaystyle{A}$ και την ευθεία $\displaystyle{Ce_1}$ φέρουμε την κάθετη από
το σημείο $\displaystyle{A}$ προς την $\displaystyle{Ce_1}$ , δηλαδή την $\displaystyle{AB}$ . Τότε σύμφωνα με το Θεώρημα των
τριών καθέτων η $\displaystyle{AB}$ θα είναι και κάθετη στο επίπεδο $\displaystyle{(p)}$ . Δηλαδή αυτό που ζητούσαμε.

(Συνεχίζεται...)

Κώστας Δόρτσιος

Christos.N · #7

Ευχαριστώ πάρα πολύ κύριε Κώστα , περιμένω την συνέχεια των σκέψεων σας, όμως κάτι κουτσοκατάφερα και εγώ και αναλύω την συλλογιστική μου πορεία όχι για να κάμψω την διάθεση σας αυτή, παρά γιατί σαν χαρούμενος μαθητής σας (που τόσες φορές με εμπνέεται με το μεράκι σας) να σας δείξω τι κατάφερα. Επίσης θα ήθελα να ευχαριστήσω τον Τάκη Χρονόπουλο που άμεσα με βοήθησε στους προβληματισμούς μου.

: foci.PNG (69.36 KiB) Προβλήθηκε 1143 φορές

Αφού γεωμετρικά προσδιορίσουμε τον μεγάλο άξονα της έλλειψης, στην συνέχεια ορίζεται τρίγωνο με κορυφές τα άκρα του μεγάλου άξονα και την κορυφή του κώνου. Το κέντρο του εγγεγραμμένου κύκλου στο τρίγωνο αυτό είναι το κέντρο της σφαίρας και ακτίνα αυτής ορίζεται άμεσα. Αντίστοιχα το κέντρο του παραγεγραμμένου κύκλου προσδιορίζει το κέντρο της σφαίρας που βρίσκεται στο έτερο ημιχώρο και αντίστοιχα η ακτίνα της.

#8

Christos.N έγραψε: ↑
Κυρ Φεβ 25, 2018 10:58 am
Ευχαριστώ πάρα πολύ κύριε Κώστα , περιμένω την συνέχεια των σκέψεων σας, όμως κάτι κουτσοκατάφερα και εγώ και αναλύω την συλλογιστική μου πορεία όχι για να κάμψω την διάθεση σας αυτή, παρά γιατί σαν χαρούμενος μαθητής σας (που τόσες φορές με εμπνέεται με το μεράκι σας) να σας δείξω τι κατάφερα. Επίσης θα ήθελα να ευχαριστήσω τον Τάκη Χρονόπουλο που άμεσα με βοήθησε στους προβληματισμούς μου.

Αφού γεωμετρικά προσδιορίσουμε τον μεγάλο άξονα της έλλειψης, στην συνέχεια ορίζεται τρίγωνο με κορυφές τα άκρα του μεγάλου άξονα και την κορυφή του κώνου. Το κέντρο του εγγεγραμμένου κύκλου στο τρίγωνο αυτό είναι το κέντρο της σφαίρας και ακτίνα αυτής ορίζεται άμεσα. Αντίστοιχα το κέντρο του παραγεγραμμένου κύκλου προσδιορίζει το κέντρο της σφαίρας που βρίσκεται στο έτερο ημιχώρο και αντίστοιχα η ακτίνα της.

Χρήστο καλησπέρα.

Το σχήμα σου είναι σωστό. Απλά θα ήθελα να εξηγήσω την πρότασή σου:
"Αφού γεωμετρικά προσδιορίσουμε τον μεγάλο άξονα της έλλειψης"
την οποία έχω χρωματίσει με κόκκινο στο ανωρέρω κείμενό σου.

Συνεχίζω λοιπόν στο ακόλουθο σχήμα:

: Άξονας έλλειψης 1.png (81.31 KiB) Προβλήθηκε 1109 φορές

Έχω ως δεδομένα μια κωνική επιφάνεια $\displaystyle{C}$ (ορθή και κυκλική) και ένα επίπεδο $\displaystyle{(P)}$ που τέμνει τον άξονά της
σε ένα σημείο $\displaystyle{O}$ .
Σύμφωνα με την προηγούμενή μου ανάρτηση μπορώ να κατασκευάσω την κάθετη από την κορυφή $\displaystyle{K}$ της κωνικής
επιφάνειας προς το επίπεδο $\displaystyle{(P)}$ , έστω την $\displaystyle{KL}$ .
Αν τώρα ενώσω το σημείο $\displaystyle{L}$ με το σημείο $\displaystyle{O}$ , τότε η ευθεία που ορίζεται τέμνει την κωνική επιφάνεια
σε δύο σημεία, έστω τα $\displaystyle{A,B}$ τα οποία ορίζουν και το μεγάλο άξονα της έλλειψης που θα προκύψει από την
τομή του επιπέδου $\displaystyle{(P)}$ με την κωνική τομή $\displaystyle{(C)}$ .
Αυτή η διαπίστωση θεμελιώνεται από το γεγονός ότι πάνω στην $\displaystyle{AB}$ θα ανήκουν οι δύο εστίες της
έλλειψης, οι οποίες θα προκύψουν από την εγγραφή των σφαιρών, όπως κι εσύ περιγράφεις. Με άλλα
λόγια οι εστίες της έλλειψης θα είναι τα σημεία επαφής των σφαιρών(εγγεγραμμένης και παρεγγεγραμμένης)
στην κωνική επιφάνεια $\displaystyle{(C)}$ και στο επίπεδο $\displaystyle{(P)}$ .

Νομίζω αυτή είναι η απάντηση που ήθελα να δώσω στο αρχικό σου ερώτημα.

Αν και είναι πλεονασμός, παραθέτω και δύο ακόμα σχήματα:
1ο Σχήμα:

: Αξονας έλλειψης2.png (82.16 KiB) Προβλήθηκε 1109 φορές

Στο σχήμα αυτό φαίνεται ο τρόπος που σχηματίζω το τρίγωνο $\displaystyle{KAB}$ από την τομή της κωνικής επιφάνειας
με το επίπεδο που ορίζεται από τον άξονα της κωνικής επιφάνειας και το σημείο $\displaystyle{L}$ .
(Το τρίγωνο αυτό βέβαια θα μπορούσε να προκύψει και ευκολώτερα ενώνοντας την κορυφή $\displaystyle{K}$ με τα σημεία
που προηγούμενα βρήκαμε, δηλαδή τα $\displaystyle{A,B}$ , χωρίς το συγκεκριμένο επίπεδο που θεωρήσαμε πριν)

2ο Σχήμα:

: Άξονας έλλειψης 3.png (119.82 KiB) Προβλήθηκε 1109 φορές

Στο σχήμα αυτό φαίνονται οι σφαίρες καθώς και οι Εστίες της έλλειψης στο μεγάλο άξονα αυτής.

Σημείωση:
Τα σχήματα έγιναν με το Cabri3D. Θα μπορούσαν να γίνουν και με το Geogebra, όπως δούλεψες κι εσύ.

Κώστας Δόρτσιος

Christos.N · #9

Αυτός είσαι Κύριε Κώστα

: κατάλογος.jpg (11.41 KiB) Προβλήθηκε 1045 φορές

#10

KDORTSI έγραψε: ↑
Κυρ Φεβ 25, 2018 10:00 pm

.................

Άξονας έλλειψης 3.png
Στο σχήμα αυτό φαίνονται οι σφαίρες καθώς και οι Εστίες της έλλειψης στο μεγάλο άξονα αυτής.
.................

Κώστας Δόρτσιος

Ενδιαφέρον στις σφαίρες Dantelin έχουν και οι διευθετούσες των κωνικών τομών.

#11

rek2 έγραψε: ↑
Τετ Φεβ 28, 2018 7:11 pm

KDORTSI έγραψε: ↑
Κυρ Φεβ 25, 2018 10:00 pm

.................

Άξονας έλλειψης 3.png
Στο σχήμα αυτό φαίνονται οι σφαίρες καθώς και οι Εστίες της έλλειψης στο μεγάλο άξονα αυτής.
.................

Κώστας Δόρτσιος
Ενδιαφέρον στις σφαίρες Dantelin έχουν και οι διευθετούσες των κωνικών τομών.

Αγαπητέ φίλε Κώστα καλησπέρα...

Πράγματι το θέμα έχει ενδιαφέρον και θα προσπαθήσω να το παρουσιάσω
για την περίπτωση της έλλειψης. Οι άλλες περιπτώσεις είναι ανάλογες.

1ο σχήμα

: Διευθετούσες 1.png (145.67 KiB) Προβλήθηκε 964 φορές

Στο σχήμα αυτό έχουμε τμήσει το αρχικό επίπεδο $\displaystyle{(P)}$ με τα επίπεδα $\displaystyle{(Q1),(Q2)}$ που ορίζουν
οι κύκλοι επαφής των δύο σφαιρών με τη δοθείσα κωνική επιφάνεια.

Οι τομές αυτές είναι οι ευθείες $\displaystyle{(d_1),(d_2)}$ και όπως θα αποδείξουμε στη συνέχεια
είναι οι διευθετούσες της έλλειψης που προέκυψε από την τομή του $\displaystyle{(P)}$ με την κωνική επιφάνεια.

Για να μη έχουμε πολύπλοκο περιβάλλον θα κρύψουμε κάποια στοιχεία
από το πρώτο σχήμα και έτσι πάμε σε ένα δεύτερο.

Σχήμα 2ο

: Διευθετούσες 2.png (76.7 KiB) Προβλήθηκε 964 φορές

Στο σχήμα αυτό θεωρούμε ένα τυχαίο σημείο $\displaystyle{M}$ της έλλειψης φέρουμε
την $\displaystyle{ME_1}$ η οποία είναι ίση με την $\displaystyle{MT}$ , όπου η $\displaystyle{MT}$ είναι εφαπτομένη
της σφαίρας που φαίνεται από το σημείο $\displaystyle{M}$ και ασφαλώς ο φορέας αυτής
διέρχεται από την κορυφή $\displaystyle{K}$ της κωνικής τομής. Δηλαδή:

$\displaystyle{ME_1=MT \ \ (1)}$

καθόσον οι εφαπτόμενες από ένα σημείο εκτός σφαίρας προς αυτήν είναι μεταξύ των ίσες.

(Η σχέση αυτή αναφέρθηκε στην πρώτη μου στο θέμα που συζητάμε)

Επίσης φέρουμε από το σημείο $\displaystyle{M}$ την κάθετη $\displaystyle{MN}$ προς την $\displaystyle{(d_1)}$ .

Έτσι για να δείξουμε ότι η $\displaystyle{(d_1)}$ είναι διευθετούσα της έλλειψης αρκεί να
δείξουμε ότι:

$\displaystyle{\frac{ME_1}{MN}=c \ \ (2)}$

Σχήμα 3ο

: Διευθετούσες 3.png (62.57 KiB) Προβλήθηκε 964 φορές

Από το σημείο $\displaystyle{M}$ φέρουμε την κάθετη $\displaystyle{MS}$ προς το επίπεδο $\displaystyle{(Q_1)}$
και τότε από τα δύο ορθογώνια τρίγωνα $\displaystyle{(MST), (MSN)}$ αντίστοιχα προκύπτουν
οι σχέσεις:

$\displaystyle{\frac{MS}{MT}=cos\phi \ \ (3)}$

$\displaystyle{\frac{MS}{MN}=sin\omega \ \ (4)}$

όπου $\displaystyle{\phi}$ είναι η γνωία που σχηματίζει ο άξονας της κωνικής επιφάνειας με μια γενέτειρά της
και $\displaystyle{\omega}$ είναι η γωνία των επιπέδων $\displaystyle{(P), (Q_1)}$ .

Διαιρώντας την (4) με την (3) προκύπτει:

$\displaystyle{\frac{MT}{MN}=\frac{sin\omega}{cos\phi} \ \ (5)}$

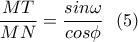
Τέλος από την (5) και την (1) προκύπτει:

$\displaystyle{\frac{ME_1}{MN}=\frac{sin\omega}{cos\phi} \ \ (6)}$

Η σχέση (6) δηλώνει ότι η $\displaystyle{(d_1)}$ είναι η διευθετούσα που αντιστοιχεί στην
εστία $\displaystyle{E_1}$ .

Όμοια εργαζόμαστε και για την άλλη εστία $\displaystyle{E_2}$ .

Σημείωση 1:
Η εκκεντρότητα της έλλειψης που μελετήσαμε είναι $\displaystyle{e=\frac{sin\omega}{cos\phi}}$

Σημείωση 2:
Κατά την ανάγνωση καλό είναι να ελεγχονται όλα τα σχήματα, ιδίως για τον έλεγχο των σχέσεων (3) και (4)
και για να δείτε καλύτερα τις γωνίες που ανάφερα. Εξάλλου για το λόγο αυτό δεν έβαλα ταυτόχρονα όλες
τις λεπτομέρειες σε ένα και μοναδικο σχήμα. Δεν ξέρω αν έτσι θα ήταν καλύτερα(;).

Κώστας Δόρτσιος

Κωνική τομή : Γιατί είναι έλλειψη ;

Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Re: Κωνική τομή : Γιατί είναι έλλειψη ;

Μέλη σε σύνδεση