Γεωμετρικός τόπος σημείων από τα όποια άγονται εφαπτομένες προς παραβολή και σχηματίζουν σταθερή γωνία

Άρης Αεράκης · #1

Με αφορμή την άσκηση 6 Α΄ομάδας της παραγράφου της παραβολής στο σχολικό βιβλίο ομάδας προσανατολισμού Β΄Λυκείου και γενικεύοντας το συμπέρασμα αυτό ανέφερα στους μαθητές ότι :

Έστω παραβολή με κορυφή την αρχή των αξόνων και εστίες στο χχ΄ (αντίστοιχα στο ψψ΄). Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν ορθή γωνία , είναι η διευθετούσα της παραβολής

Τότε ένας μαθητής με ρώτησε αν υπάρχει αντίστοιχος γεωμετρικός τόπος για οξεία γωνία ή για αμβλεία γωνία. Ομολόγησα ότι δεν το ήξερα και του είπα ότι θα το ψάξω.

Το έψαξα και βρήκα το εξής :
α) Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν σταθερή οξεία γωνία ω, είναι κλάδος υπερβολής
β) Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν σταθερή αμβλεία γωνία ω, είναι ο άλλος κλάδος της ίδιας υπερβολής

Επίσης με το geogebra παρατηρούμε (χωρίς να το έχω αποδείξει) ότι :

1) η μία εστία της υπερβολής ταυτίζεται με την εστία της παραβολής
2) η μία γωνία των ασυμπτώτων της υπερβολής είναι η γωνία ω και άρα είναι ανεξάρτητη από την παράμετρο p της παραβολής
3) η εκκεντρότητα της υπερβολής εξαρτάται μόνο από τη γωνία ω και όχι από την παράμετρο ρ της παραβολής

Δεν γνωρίζω αν τα παραπάνω γενικευόνται για όλες τις παραβολές.

Δεν ξέρω αν το θέμα είναι γενικώς γνωστό. Το δημοσιεύω επειδή μου φάνηκε ενδιαφέρον, αλλά και γιατί ένας μαθητής με παρακίνησε να ψάξω κάτι που προσωπικά μέχρι τότε δε με είχε ποτέ προβληματίσει.

Al.Koutsouridis · #2

Άρης Αεράκης έγραψε:

Το έψαξα και βρήκα το εξής :
α) Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν σταθερή οξεία γωνία ω, είναι κλάδος υπερβολής
β) Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν σταθερή αμβλεία γωνία ω, είναι ο άλλος κλάδος της ίδιας υπερβολής

Επίσης με το geogebra παρατηρούμε (χωρίς να το έχω αποδείξει) ότι :

1) η μία εστία της υπερβολής ταυτίζεται με την εστία της παραβολής
2) η μία γωνία των ασυμπτώτων της υπερβολής είναι η γωνία ω και άρα είναι ανεξάρτητη από την παράμετρο p της παραβολής
3) η εκκεντρότητα της υπερβολής εξαρτάται μόνο από τη γωνία ω και όχι από την παράμετρο ρ της παραβολής

Δεν γνωρίζω αν τα παραπάνω γενικευόνται για όλες τις παραβολές.

Δεν ξέρω αν το θέμα είναι γενικώς γνωστό. Το δημοσιεύω επειδή μου φάνηκε ενδιαφέρον, αλλά και γιατί ένας μαθητής με παρακίνησε να ψάξω κάτι που προσωπικά μέχρι τότε δε με είχε ποτέ προβληματίσει.

Καλησπέρα,

Ναι νομίζω είναι σχετικά γνωστό π.χ. εδώ (στα ρώσικα) Θεώρημα 1.18 σελ 25, σίγουρα και σε άλλα βιβλία.

"Ο γεωμετρικός τόπος των σημείων από τα οποία παραβολή φαίνεται υπό σταθερή γωνία $\phi$ ή $180^{0} -\phi$ είναι υπερβολή με εστία και διευθετούσα αυτή της παραβολής"

Η απόδειξη βασίζεται στο παρακάτω λήμμα:

Λήμμα: Το σημείο τομής δυο εφαπτομένων σε παραβολή είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου που σχηματίζεται από τις προβολές των σημείων επαφής αυτών των εφαπτομένων στην διευθετούσα και την εστία της.

: geometrikos_topos_tomhs_ef_paravolhs.png (71.15 KiB) Προβλήθηκε 1093 φορές

Η απόδειξη του παραπάνω λήμματος είναι σχετικά απλή. Ως γνωστόν τα συμμετρικά σημεία της εστίας μιας παραβολής βρίσκονται επί της διευθετούσας ή αλλιώς οι εφαπτομένες είναι μεσοκάθετοι των τμημάτων FX{'}

και

. Οπότε και το

είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου FX{'}Y{'}

.

Ως αναφορά τα ερωτήματα (α), (β) και (1), (2), (3) έχουμε. Οι εφαπτομένες και οι ευθείες FX{'}, FY{'}

σχηματίζουν ένα εγγράψιμο τετράπλευρο άρα θα είναι $\angle X{'}FY{'} = 180-\phi$ και για την αντίστοιχη επίκεντρη γωνία $\angle X{'}PY{'} = 360^{0}-2\phi$ .

Από τα παραπάνω αν

η διευθετούσα της παραβολής τότε η απόσταση του σημείου

από αυτήν, έστω

, θα είναι

$Pl = X{'}P \cdot| \cos (180^0-\phi) |= FP \cdot| \cos (180^0-\phi) | = FP \cdot |\cos \phi|$

Από τον ορισμό της υπερβολής με χρήση δειυθετούσας π.χ. εδώ στη παράγραφο Definition of a hyperbola by the directrix property, έχουμε

$\dfrac{FP}{Pl} = \dfrac{1}{|\cos \phi|} = const> 1$

Δηλαδή το σημείο

είναι σημείο υπερβολής με εστία το

και διευθετούσα

όπως και η παραβολή. Η εκκεντρότητά της είναι ίση με $\epsilon = \dfrac{1}{\cos \phi}$ οπότε και η γωνία μεταξύ των ασύμπτώτων θα είναι $2 \phi$ και όλα τα ερωτήματα έχουν απαντηθεί.

Σαν σχόλιο να αναφέρω ότι το συγκεκριμένο πρόβλημα είναι ένα καλό παράδειγμα το πως διαφορετικοί ορισμοί μιας έννοιας μπορούν να οδηγήσουν σε διαφορετικές λύσεις. Ίσως ο ορισμός των κωνικών με χρήση διευθετούσας θα έπρεπε να υπάρχει στο σχολικό βιβλίο σαν άσκηση Β' ομάδας π.χ. Καθώς και σε κάποιο ιστορικό πλαίσιο το πως ακριβώς η τομή του κώνου με επίπεδο είναι όντος παραβολή, έλλειψη, υπερβολή με τους ορισμούς της αναλυτικής γεωμετρίας (ένας μικρός φόρος τιμής στους προγόνους μας).

Άρης Αεράκης · #3

Μια απόδειξη στον παρακάτω σύνδεσμο : http://eclass.sch.gr/modules/document/i ... d8362bQKit

#4

Άρης Αεράκης έγραψε:Με αφορμή την άσκηση 6 Α΄ομάδας της παραγράφου της παραβολής στο σχολικό βιβλίο ομάδας προσανατολισμού Β΄Λυκείου και γενικεύοντας το συμπέρασμα αυτό ανέφερα στους μαθητές ότι :

Έστω παραβολή με κορυφή την αρχή των αξόνων και εστίες στο χχ΄ (αντίστοιχα στο ψψ΄). Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν ορθή γωνία , είναι η διευθετούσα της παραβολής

Τότε ένας μαθητής με ρώτησε αν υπάρχει αντίστοιχος γεωμετρικός τόπος για οξεία γωνία ή για αμβλεία γωνία. Ομολόγησα ότι δεν το ήξερα και του είπα ότι θα το ψάξω.

Το έψαξα και βρήκα το εξής :
α) Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν σταθερή οξεία γωνία ω, είναι κλάδος υπερβολής
β) Ο γεωμετρικός τόπος των σημείων του επιπέδου από τα οποία άγονται εφαπτομένες προς την παραπάνω παραβολή και σχηματίζουν σταθερή αμβλεία γωνία ω, είναι ο άλλος κλάδος της ίδιας υπερβολής

Επίσης με το geogebra παρατηρούμε (χωρίς να το έχω αποδείξει) ότι :

1) η μία εστία της υπερβολής ταυτίζεται με την εστία της παραβολής
2) η μία γωνία των ασυμπτώτων της υπερβολής είναι η γωνία ω και άρα είναι ανεξάρτητη από την παράμετρο p της παραβολής
3) η εκκεντρότητα της υπερβολής εξαρτάται μόνο από τη γωνία ω και όχι από την παράμετρο ρ της παραβολής

Δεν γνωρίζω αν τα παραπάνω γενικευόνται για όλες τις παραβολές.

Δεν ξέρω αν το θέμα είναι γενικώς γνωστό. Το δημοσιεύω επειδή μου φάνηκε ενδιαφέρον, αλλά και γιατί ένας μαθητής με παρακίνησε να ψάξω κάτι που προσωπικά μέχρι τότε δε με είχε ποτέ προβληματίσει.

Το θέμα έχει ξανασυζητηθεί στο πριν μερικά χρόνια αλλά πιο εύκολα το ξαναγράφω αντί να το βρώ. Ο Θανάσης ο KARKAR το είχε θέσει αν θυμάμαι και μάλλον αυτός θα το βρεί καλύτερα.

Αν είναι τα σημεία επαφής των εκ του $S\left( {{x}_{0}},{{y}_{0}} \right)$ με την παραβολή $\left( C \right)\to {{y}^{2}}=2px$ τότε η είναι η πολική του ως προς την παραβολή και συνεπώς έχει εξίσωση $y{{y}_{0}}=p\left( x+{{x}_{0}} \right)$ οπότε οι συντεταγμένες των θα προκύψουν από τη λύση του συστήματος

$\left\{ \begin{gathered} y{y_0} = p\left( {x + {x_0}} \right) \\ {y^2} = 2px \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} y{y_0} = px + p{x_0} \\ {y^2} = 2px \\ \end{gathered} \right. \Leftrightarrow$ $\left\{ \begin{gathered} y{y_0} - p{x_0} = px \\ {y^2} = 2px \\ \end{gathered} \right. \Leftrightarrow \ldots \left\{ \begin{gathered} y{y_0} - p{x_0} = px \\ \boxed{{y^2} - 2y{y_0} + 2p{x_0} = 0}:\left( 1 \right) \\ \end{gathered} \right.$ .
[attachment=0]4.png[/attachment]
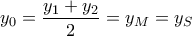Αν ${{y}_{1}},{{y}_{2}}$ είναι οι ρίζες της $\left( 1 \right)$ (τεταγμένες των αντίστοιχα) τότε ${{y}_{1}}{{y}_{2}}=2p{{x}_{0}},{{y}_{1}}+{{y}_{2}}=2p{{y}_{0}}$ (από τους τύπους του Vieta) και με ${{y}_{0}}=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}={{y}_{M}}={{y}_{S}}$ προκύπτει ότι $SM\parallel {x}'x$ και από την ανακλαστική ιδιότητα της παραβολής προκύπτει άμεσα ότι $\angle AEB=2\left( \angle ASB \right)=2\varphi$ όπου $E\left( \dfrac{p}{2},0 \right)$ η εστία της παραβολής

$\overrightarrow {EA} = \left( {{x_1} - \dfrac{p}{2},{y_1}} \right)\,\,\,\& \,\,\,\overrightarrow {EB} = \left( {{x_2} - \dfrac{p}{2},{y_2}} \right),\left| {\overrightarrow {EA} } \right|$ $= \sqrt {{{\left( {{x_1} - \dfrac{p}{2}} \right)}^2} + y_1^2} = \left| {{x_1} + \dfrac{p}{2}} \right| = \left| {\dfrac{{y_1^2}}{{2p}} + \dfrac{p}{2}} \right| = \dfrac{{y_1^2 + {p^2}}}{{2\left| p \right|}}$ $\left| {\overrightarrow {EB} } \right| = \ldots \dfrac{{y_2^2 + {p^2}}}{{2\left| p \right|}}$ .

$\overrightarrow {EA} \cdot \overrightarrow {EB} = \left( {{x_1} - \dfrac{p}{2}} \right)\left( {{x_2} - \dfrac{p}{2}} \right) + {y_1}{y_2} = {x_1}{x_2} - \dfrac{p}{2}\left( {{x_1} + {x_2}} \right) + \dfrac{{{p^2}}}{4} + {y_1}{y_2}$ $= \dfrac{{{{\left( {{y_1}{y_2}} \right)}^2}}}{{4{p^2}}} - \dfrac{p}{2}\left( {\dfrac{{y_1^2 + y_2^2}}{{2p}}} \right) + \dfrac{{{p^2}}}{4} + {y_1}{y_2}$

$= \dfrac{{{{\left( {{y_1}{y_2}} \right)}^2}}}{{4{p^2}}} - \dfrac{p}{2}\left( {\dfrac{{{{\left( {{y_1} + {y_2}} \right)}^2} - 2{y_1}{y_2}}}{{2p}}} \right) + \dfrac{{{p^2}}}{4} + {y_1}{y_2} =$ $\dfrac{{4{p^2}x_0^2}}{{4{p^2}}} - \dfrac{1}{4}\left[ {4y_0^2 - 4p{x_0}} \right] + \dfrac{{{p^2}}}{4} + 2p{x_0} =$ $x_0^2 - y_0^2 + 3p{x_0} + \dfrac{{{p^2}}}{4}$

$\left| {\overrightarrow {EA} } \right| \cdot \left| {\overrightarrow {EB} } \right| = \dfrac{{y_1^2 + {p^2}}}{{2\left| p \right|}} \cdot \dfrac{{y_2^2 + {p^2}}}{{2\left| p \right|}} = \dfrac{{{{\left( {{y_1}{y_2}} \right)}^2} + {p^2}\left( {y_1^2 + y_2^2} \right) + {p^4}}}{{4{p^2}}}$ $= x_0^2 + \dfrac{1}{4}\left[ {4y_0^2 - 4p{x_0} + {p^2}} \right] = x_0^2 + y_0^2 - p{x_0} + \dfrac{{{p^2}}}{4}$ .

$k = \cos 2\varphi = \dfrac{{x_0^2 - y_0^2 + 3p{x_0} + \dfrac{{{p^2}}}{4}}}{{x_0^2 + y_0^2 - p{x_0} + \dfrac{{{p^2}}}{4}}} \Leftrightarrow$ $\boxed{\left( {k - 1} \right)x_0^2 + \left( {k + 1} \right)y_0^2 - p\left( {k + 3} \right){x_0} + \left( {k - 1} \right)\dfrac{{{p^2}}}{4} = 0}:\left( 2 \right)$ .

Στάθης

Al.Koutsouridis · #5

Να σημειώσω ότι συμπλήρωσα την αρχική μου ανάρτηση με την πλήρη λύση των ερωτημάτων που τέθηκαν αρχικά (λόγω έλλειψης χρόνου δεν το έκανα το βράδυ).

Γεωμετρικός τόπος σημείων από τα όποια άγονται εφαπτομένες προς παραβολή και σχηματίζουν σταθερή γωνία

Γεωμετρικός τόπος σημείων από τα όποια άγονται εφαπτομένες προς παραβολή και σχηματίζουν σταθερή γωνία

Re: Γεωμετρικός τόπος σημείων από τα όποια άγονται εφαπτομένες προς παραβολή και σχηματίζουν σταθερή γωνία

Re: Γεωμετρικός τόπος σημείων από τα όποια άγονται εφαπτομένες προς παραβολή και σχηματίζουν σταθερή γωνία

Re: Γεωμετρικός τόπος σημείων από τα όποια άγονται εφαπτομένες προς παραβολή και σχηματίζουν σταθερή γωνία

Re: Γεωμετρικός τόπος σημείων από τα όποια άγονται εφαπτομένες προς παραβολή και σχηματίζουν σταθερή γωνία

Μέλη σε σύνδεση