KARKAR έγραψε: β) ( Προαιρετικό ) Θα λέγατε το ίδιο για οποιαδήποτε έλλειψη ;
Ας εξετάσουμε λοιπόν το γενικότερο πρόβλημα για έλλειψη με εξίσωση


- Βελτιωμένος τόπος.β.png (23.88 KiB) Προβλήθηκε 662 φορές
Τα σημεία τομής της εφαπτομένης

με τις ευθείες

είναι αντίστοιχα

Έχουμε λοιπόν τις παρακάτω εξισώσεις ευθειών:

και το σημείο τομής τους είναι

Επειδή τώρα το σημείο

επαληθεύει την εξίσωση της αρχικής έλλειψης, με απαλοιφή βρίσκουμε ότι
ο ζητούμενος γεωμετρικός τόπος είναι έλλειψη με εξίσωση
 Ίσως η παρατήρηση ότι
Ίσως η παρατήρηση ότι  απλουστεύει τη λύση του προβλήματος.
απλουστεύει τη λύση του προβλήματος. , φέραμε τις εφαπτόμενες στα άκρα
, φέραμε τις εφαπτόμενες στα άκρα  του μικρού άξονα .
του μικρού άξονα . τέμνει τις παραπάνω ευθείες στα
τέμνει τις παραπάνω ευθείες στα  .
. των
των  .
.

 Έστω
Έστω  το σημείο επαφής. Η εξίσωση της εφαπτομένης είναι:
το σημείο επαφής. Η εξίσωση της εφαπτομένης είναι: και τέμνει τις ευθείες
και τέμνει τις ευθείες 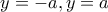 στα σημεία
στα σημεία  αντίστοιχα.
αντίστοιχα.

 με τις ευθείες
με τις ευθείες  είναι αντίστοιχα
είναι αντίστοιχα  Έχουμε λοιπόν τις παρακάτω εξισώσεις ευθειών:
Έχουμε λοιπόν τις παρακάτω εξισώσεις ευθειών: και το σημείο τομής τους είναι
και το σημείο τομής τους είναι 
 επαληθεύει την εξίσωση της αρχικής έλλειψης, με απαλοιφή βρίσκουμε ότι
επαληθεύει την εξίσωση της αρχικής έλλειψης, με απαλοιφή βρίσκουμε ότι 
 απλουστεύει τη λύση του προβλήματος.
απλουστεύει τη λύση του προβλήματος.