Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
Συντονιστής: Τηλέγραφος Κώστας
 Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
Ξέρει κανείς που μπορώ να βρω τις αποδείξεις των ιδιοτήτων
(2) (λ+μ)*𝙖=λ*𝙖+μ*𝙖
(3) λ*(μ*𝙖)=(λ*μ)*𝙖
του πολλαπλασιασμού αριθμού με διάνυσμα στην παράγραφο 1.3 του βιβλίου κατεύθυνσης;
Προσπαθώ μάταια εδώ και λίγο καιρό να τις κάνω μόνος μου, αλλά δεν τα κατάφερα. Ευχαριστώ.
(2) (λ+μ)*𝙖=λ*𝙖+μ*𝙖
(3) λ*(μ*𝙖)=(λ*μ)*𝙖
του πολλαπλασιασμού αριθμού με διάνυσμα στην παράγραφο 1.3 του βιβλίου κατεύθυνσης;
Προσπαθώ μάταια εδώ και λίγο καιρό να τις κάνω μόνος μου, αλλά δεν τα κατάφερα. Ευχαριστώ.
Λέξεις Κλειδιά:
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
Έστω
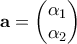 . Τότε,
. Τότε,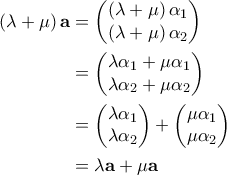
Μπορείς να αποδείξεις την άλλη;
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Al.Koutsouridis
- Δημοσιεύσεις: 1810
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
Νομίζω η παραπάνω απόδειξη δεν είναι ενδεδειγμένη, για την εύλογη απορία ενός μαθητή.
Από την μία ο συμβολισμός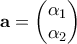 δεν υπάρχει στο σχολικό βιβλίο και από την άλλη οι συντεταγμένες διανύσματος εισάγονται στην επόμενη ενότητα.
δεν υπάρχει στο σχολικό βιβλίο και από την άλλη οι συντεταγμένες διανύσματος εισάγονται στην επόμενη ενότητα.
Από την μία ο συμβολισμός
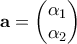 δεν υπάρχει στο σχολικό βιβλίο και από την άλλη οι συντεταγμένες διανύσματος εισάγονται στην επόμενη ενότητα.
δεν υπάρχει στο σχολικό βιβλίο και από την άλλη οι συντεταγμένες διανύσματος εισάγονται στην επόμενη ενότητα.- nsmavrogiannis
- Επιμελητής
- Δημοσιεύσεις: 4456
- Εγγραφή: Σάβ Δεκ 20, 2008 7:13 pm
- Τοποθεσία: Αθήνα
- Επικοινωνία:
Re: Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
'Ισως για αυτό που ρωτάτε βρείτε χρήσιμο το βιβλίοΠετρακας έγραψε: ↑Τετ Οκτ 18, 2023 9:19 pmΞέρει κανείς που μπορώ να βρω τις αποδείξεις των ιδιοτήτων
(2) (λ+μ)*𝙖=λ*𝙖+μ*𝙖
(3) λ*(μ*𝙖)=(λ*μ)*𝙖
του πολλαπλασιασμού αριθμού με διάνυσμα στην παράγραφο 1.3 του βιβλίου κατεύθυνσης;
Προσπαθώ μάταια εδώ και λίγο καιρό να τις κάνω μόνος μου, αλλά δεν τα κατάφερα. Ευχαριστώ.
Ιω. Πανάκης Στοιχεία Διανυσματικού Λογισμού
που μπορεί να μεταφορτωθεί από τον σύνδεσμο
https://drive.google.com/file/d/1WkPGbH ... sp=sharing
που υπάρχει στην σελίδα που διατηρεί ο συνάδελφος Π. Χρονόπουλος (https://parmenides52.blogspot.com/)
Αν κανείς δεν ελπίζει, δεν θα βρεί το ανέλπιστο, οι δρόμοι για το ανεξερεύνητο θα είναι κλειστοί.
Ηράκλειτος
Ηράκλειτος
Re: Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
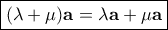
Απόδειξη.
(α) Έστω
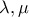 θετικοί πραγματικοί αριθμοί.
θετικοί πραγματικοί αριθμοί.Το διάνυσμα
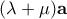 είναι ομόρροπο του
είναι ομόρροπο του 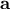 με
με 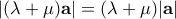 .
.Το διάνυσμα
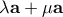 είναι ομόρροπο του
είναι ομόρροπο του 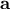 με
με 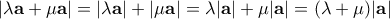 .
.Έτσι τα διανύσματα
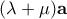 και
και 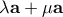 είναι ομόρροπα με το ίδιο μέτρο και συνεπώς ίσα.
είναι ομόρροπα με το ίδιο μέτρο και συνεπώς ίσα.(β) Έστω
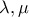 αρνητικοί πραγματικοί αριθμοί.
αρνητικοί πραγματικοί αριθμοί.Το διάνυσμα
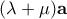 είναι αντίρροπο του
είναι αντίρροπο του 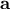 με
με 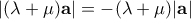 .
.Το διάνυσμα
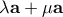 είναι αντίρροπο του
είναι αντίρροπο του 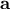 με
με 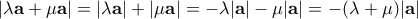 .
.Έτσι τα διανύσματα
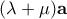 και
και 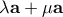 είναι ομόρροπα με το ίδιο μέτρο και συνεπώς ίσα.
είναι ομόρροπα με το ίδιο μέτρο και συνεπώς ίσα.(γ) Έστω
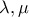 ετερόσημοι πραγματικοί αριθμοί. Χωρίς βλάβη της γενικότητας
ετερόσημοι πραγματικοί αριθμοί. Χωρίς βλάβη της γενικότητας 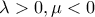
- i) Αν
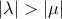 υπάρχει
υπάρχει 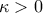 ώστε
ώστε 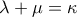
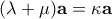
και
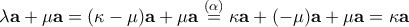
Άρα
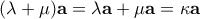
- ii) Αν
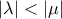 υπάρχει
υπάρχει 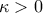 ώστε
ώστε 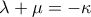
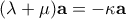
και
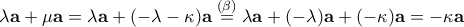
Άρα
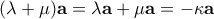
- iii) Αν
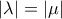 δηλαδή
δηλαδή 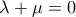 τότε και τα δύο διανύσματα είναι τα μηδενικά.
τότε και τα δύο διανύσματα είναι τα μηδενικά.
αν κάποιος από τους
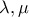 είναι το
είναι το 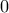 , η ισότητα είναι προφανής.
, η ισότητα είναι προφανής.

Re: Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
Σε ευχαριστώ για την απάντηση. Ευτυχώς πέτυχα τις πρώτες δύο περιπτώσεις (και την μ ή λ=0), αλλά την γ) δεν νομίζω να την έβρισκα. Δεν μπορούσα να αποδείξω την φορά του λ*Α+μ*Α. Το έβλεπα μόνο διαισθητικά. Ξεκαθάρισα έτσι και την τρίτη ιδιότητα. Και πάλι σε ευχαριστώ.abgd έγραψε: ↑Παρ Οκτ 20, 2023 8:31 pm
Απόδειξη.
(α) Έστωθετικοί πραγματικοί αριθμοί.
Το διάνυσμαείναι ομόρροπο του
με
.
Το διάνυσμαείναι ομόρροπο του
με
.
Έτσι τα διανύσματακαι
είναι ομόρροπα με το ίδιο μέτρο και συνεπώς ίσα.
(β) Έστωαρνητικοί πραγματικοί αριθμοί.
Το διάνυσμαείναι αντίρροπο του
με
.
Το διάνυσμαείναι αντίρροπο του
με
.
Έτσι τα διανύσματακαι
είναι ομόρροπα με το ίδιο μέτρο και συνεπώς ίσα.
(γ) Έστωετερόσημοι πραγματικοί αριθμοί. Χωρίς βλάβη της γενικότητας
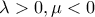
- i) Αν
υπάρχει
ώστε
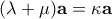
και
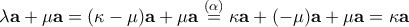
Άρα
- ii) Αν
υπάρχει
ώστε
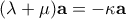
και
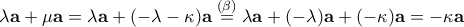
Άρα
Τέλος,
- iii) Αν
δηλαδή
τότε και τα δύο διανύσματα είναι τα μηδενικά.
αν κάποιος από τουςείναι το
, η ισότητα είναι προφανής.
- Al.Koutsouridis
- Δημοσιεύσεις: 1810
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ιδιότητες πολλαπλασιασμού αριθμού με διάνυσμα
Κατά την άποψή μου υπάρχουν δυο "θέματα" που εισάγουν, θα έλεγα τεχνητά, δυσκολία στην απόδειξη αυτής της πρότασης.
α) Το πρώτο έχει να κάνει με την σειρά και την φορά που δίνονται οι ιδιότητες, δεδομένου των ενοτήτων που έχουν προηγηθεί. Πιό καλά θα ήταν να δοθούν ως:
1)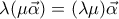
2)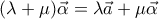
3)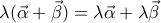
και μάλιστα με την αντίθετη φορά στις ισότητες, δηλαδή:
1)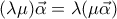
2)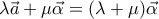
3)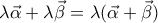
Ιδιαίτερα για την ιδίοτητα (2) καθώς η έκφραση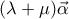 εισάγει δυσκολία στην κατανόηση καθώς εμφανίζεται πρώτη φορά. Και ασυναίσθητα βάζουμε τον μαθητή, με την σειρά που έχουν δοθεί τα δυο μέλη της ισότητας, να εξάγει από αυτήν το δεύτερο μέλος.
εισάγει δυσκολία στην κατανόηση καθώς εμφανίζεται πρώτη φορά. Και ασυναίσθητα βάζουμε τον μαθητή, με την σειρά που έχουν δοθεί τα δυο μέλη της ισότητας, να εξάγει από αυτήν το δεύτερο μέλος.
Σε αντίθεση με το δεύτερο μέλος που είναι οικείο. Ο πολλαπλασιασμός αριθμού με διάνυσμα έχει ορισθεί στην αμέσος προηγούμενη παράγραφο και το άθροισμα διανυσμάτων στην προηγούμενη ενότητα (1.2). Κάνοντας έτσι κατανοητό από που προς τα που οδεύουμε.
Οι ιδιότητες αυτές με την μορφή που τις έχει το σχολικό βιβλίο, συνήθως εισάγωνται όταν τις δεχόμαστε αξιωματικά (Αξιώματα Weyl).
β) Το δεύτερο έχει να κάνει με το άθροισμα συγγραμμικών διανυσμάτων. Παρότι στην ενότητα 1.2 έχει δοθεί ο ορισμός του αθροίσματος διανυσμάτων στη γενική τους μορφή δεν έχει γίνει μνεία στην ειδική περίπτωση των συγραμμικών διανυσμάτων ούτε στις ιδιότητες, ούτε στις εφαρμογές, ούτε στις ασκήσεις. Αν και θα περίμενε κανείς να αρχίσει η έννοια τους αθροίσματος από εκεί.
Ο μαθητής "παιρνώντας" από το κεφάλαιο και δεδομένου ότι μαθαίνει μια καινούργια έννοια δεν έχει δει, οπτικά τουλάχιστον, τι είναι ο κανόνας παραλληλογράμμου στην εκφυλισμένη περίπτωση που τα διανύσματα είναι συγγραμμικά. Ποιές περιπτώσεις προκύπτουν στην άθροιση (ομόρροπα, αντίρροπα, όταν το μέτρο του ένος είναι μεγαλύτερο του άλλου κτλ).
Αν ακολουθεί η παραπάνω διαδικασία (α), (β) νομίζω η απόδειξη της ιδιότητας (2) θα έρθει με ένα πιο φυσικό τρόπο.
α) Το πρώτο έχει να κάνει με την σειρά και την φορά που δίνονται οι ιδιότητες, δεδομένου των ενοτήτων που έχουν προηγηθεί. Πιό καλά θα ήταν να δοθούν ως:
1)
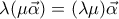
2)
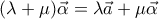
3)
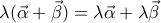
και μάλιστα με την αντίθετη φορά στις ισότητες, δηλαδή:
1)
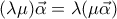
2)
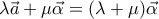
3)
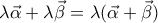
Ιδιαίτερα για την ιδίοτητα (2) καθώς η έκφραση
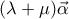 εισάγει δυσκολία στην κατανόηση καθώς εμφανίζεται πρώτη φορά. Και ασυναίσθητα βάζουμε τον μαθητή, με την σειρά που έχουν δοθεί τα δυο μέλη της ισότητας, να εξάγει από αυτήν το δεύτερο μέλος.
εισάγει δυσκολία στην κατανόηση καθώς εμφανίζεται πρώτη φορά. Και ασυναίσθητα βάζουμε τον μαθητή, με την σειρά που έχουν δοθεί τα δυο μέλη της ισότητας, να εξάγει από αυτήν το δεύτερο μέλος.Σε αντίθεση με το δεύτερο μέλος που είναι οικείο. Ο πολλαπλασιασμός αριθμού με διάνυσμα έχει ορισθεί στην αμέσος προηγούμενη παράγραφο και το άθροισμα διανυσμάτων στην προηγούμενη ενότητα (1.2). Κάνοντας έτσι κατανοητό από που προς τα που οδεύουμε.
Οι ιδιότητες αυτές με την μορφή που τις έχει το σχολικό βιβλίο, συνήθως εισάγωνται όταν τις δεχόμαστε αξιωματικά (Αξιώματα Weyl).
β) Το δεύτερο έχει να κάνει με το άθροισμα συγγραμμικών διανυσμάτων. Παρότι στην ενότητα 1.2 έχει δοθεί ο ορισμός του αθροίσματος διανυσμάτων στη γενική τους μορφή δεν έχει γίνει μνεία στην ειδική περίπτωση των συγραμμικών διανυσμάτων ούτε στις ιδιότητες, ούτε στις εφαρμογές, ούτε στις ασκήσεις. Αν και θα περίμενε κανείς να αρχίσει η έννοια τους αθροίσματος από εκεί.
Ο μαθητής "παιρνώντας" από το κεφάλαιο και δεδομένου ότι μαθαίνει μια καινούργια έννοια δεν έχει δει, οπτικά τουλάχιστον, τι είναι ο κανόνας παραλληλογράμμου στην εκφυλισμένη περίπτωση που τα διανύσματα είναι συγγραμμικά. Ποιές περιπτώσεις προκύπτουν στην άθροιση (ομόρροπα, αντίρροπα, όταν το μέτρο του ένος είναι μεγαλύτερο του άλλου κτλ).
Αν ακολουθεί η παραπάνω διαδικασία (α), (β) νομίζω η απόδειξη της ιδιότητας (2) θα έρθει με ένα πιο φυσικό τρόπο.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες
