Αν
 με
με  τότε να αποδείξετε ότι:
τότε να αποδείξετε ότι: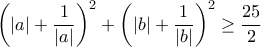
Συντονιστής: chris_gatos
 με
με  τότε να αποδείξετε ότι:
τότε να αποδείξετε ότι: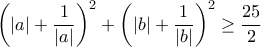
 που ισχύει για κάθε
που ισχύει για κάθε  .
. και για
και για  παίρνουμε ότι:
παίρνουμε ότι:![\displaystyle{2\left[ {{{\left( {\left| a \right| + \tfrac{1}{{\left| a \right|}}} \right)}^2} + {{\left( {\left| b \right| + \tfrac{1}{{\left| b \right|}}} \right)}^2}} \right] \geqslant {\left( {\left| a \right| + \tfrac{1}{{\left| a \right|}} + \left| b \right| + \tfrac{1}{{\left| b \right|}}} \right)^2} = {\left( {1 + \tfrac{1}{{\left| a \right|}} + \tfrac{1}{{\left| b \right|}}} \right)^2} \Rightarrow } \displaystyle{2\left[ {{{\left( {\left| a \right| + \tfrac{1}{{\left| a \right|}}} \right)}^2} + {{\left( {\left| b \right| + \tfrac{1}{{\left| b \right|}}} \right)}^2}} \right] \geqslant {\left( {\left| a \right| + \tfrac{1}{{\left| a \right|}} + \left| b \right| + \tfrac{1}{{\left| b \right|}}} \right)^2} = {\left( {1 + \tfrac{1}{{\left| a \right|}} + \tfrac{1}{{\left| b \right|}}} \right)^2} \Rightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/085be586b8fc573bc1dbcec15d2defc3.png)
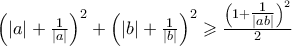
 και το ζητούμενο εδείχθη
και το ζητούμενο εδείχθη και
και  και έχουμε
και έχουμε  οπότε
οπότε 
 παίρνει τη μέγιστη τιμή του (εφόσον
παίρνει τη μέγιστη τιμή του (εφόσον  ) για
) για 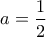 οπότε το
οπότε το  παίρνει την ελάχιστη τιμή του που ισούται με
παίρνει την ελάχιστη τιμή του που ισούται με  .
. που είναι πάντα θετικό παίρνει την ελάχιστη τιμή του που είναι
που είναι πάντα θετικό παίρνει την ελάχιστη τιμή του που είναι  για
για 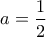 και επομένως από τα προηγούμενα προκύπτει ότι
και επομένως από τα προηγούμενα προκύπτει ότι

 ,
, 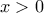 είναι κυρτή στο
είναι κυρτή στο 
 και
και  για κάθε
για κάθε 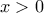 .
.  , για κάθε
, για κάθε  (1)
(1) ,
,  στην (1) παιρνουμε:
στην (1) παιρνουμε: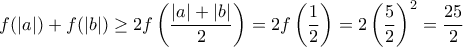
Νίκο αυτή ήταν και η δική μου λύση.Ευχαριστώ πολύ!Math Rider έγραψε:Ακόμα μία:
Η συνάρτηση,
είναι κυρτή στο

αφούκαι
για κάθε
.
Άρα από την ανισότητα Jensen έχουμε ότι, για κάθε
(1)
Έτσι για,
στην (1) παιρνουμε:
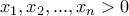 με
με 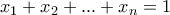 , τότε
, τότε 
 με
με  και
και  , τότε
, τότε 
Χρησιμοποιώντας την Andreescu λαμβάνουμε:matha έγραψε: 1) Ανμε
, τότε

 άρα αρκεί
άρα αρκεί  , η οποία ισχύει από την Andreescu επίσης.
, η οποία ισχύει από την Andreescu επίσης.![\displaystyle \sqrt[a]{2^{a-1}\left(\left(x+\frac{1}{x} \right)^a+\left(y+\frac{1}{y} \right)^a \right)}\geqslant x+\frac{1}{x}+y+\frac{1}{y}=1+\frac{1}{x}+\frac{1}{y}\geqslant 1+\frac{4}{x+y} \displaystyle \sqrt[a]{2^{a-1}\left(\left(x+\frac{1}{x} \right)^a+\left(y+\frac{1}{y} \right)^a \right)}\geqslant x+\frac{1}{x}+y+\frac{1}{y}=1+\frac{1}{x}+\frac{1}{y}\geqslant 1+\frac{4}{x+y}](/forum/ext/geomar/texintegr/latexrender/pictures/5f64478fed28477715cfbbd7806dd5b4.png) .
. .
.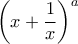 που είναι κυρτή καθώς
που είναι κυρτή καθώς 
Παραθέτω και τη δική μου αντιμετώπιση (ίσως λίγο καθυστερημένα αλλά τώρα μου <<ήρθε η έμπνευση>>chris_gatos έγραψε:Είναι γνωστή από πολλά βιβλία.Έχει πολλούς και όμορφους και διδακτικούς τρόπους απόδειξης.
Ανμε
τότε να αποδείξετε ότι:


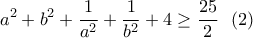

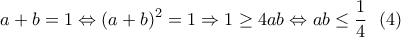


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες