Επιπλέον στην εξέταση του ΑΣΕΠ δείχνεται μία προτίμηση σε ιστορικά θέματα ή σε θέματα με ονοματεπώνυμο.
Το παρακάτω φέρει το όνομα του Euler.(διάσημη ισότητα σε τρίγωνο)
Αν Ο και Ι είναι τα κέντρα του περιγεγραμμένου και του εγγεγραμμένου κύκλου αντίστοιχα ενός τριγώνου ΑΒΓ
και R , r οι ακτίνες τους (αντίστοιχα) τότε να αποδείξετε πως:

Απο αποδείξεις κυκλοφορούν πολλές.
Ότι προαιρείσθε λοιπόν!

 τέμνει τον περιγεγραμμένο κύκλο στο
τέμνει τον περιγεγραμμένο κύκλο στο  τότε φέρουμε τη διάμετρο του περιγεγραμμένου κύκλου που διέρχεται απο το
τότε φέρουμε τη διάμετρο του περιγεγραμμένου κύκλου που διέρχεται απο το  .Ισχύει
.Ισχύει  και φέρουμε
και φέρουμε  .Απο το γενικευμένο Πυθαγόρειο θεώρημα έχουμε:
.Απο το γενικευμένο Πυθαγόρειο θεώρημα έχουμε:

 γίνεται:
γίνεται:
 και
και  είναι τα κέντρα του περιγεγραμμένου και του εγγεγραμμένου κύκλου αντίστοιχα ενός τριγώνου
είναι τα κέντρα του περιγεγραμμένου και του εγγεγραμμένου κύκλου αντίστοιχα ενός τριγώνου  και
και  οι ακτίνες τους (αντίστοιχα) τότε να αποδείξετε πως:
οι ακτίνες τους (αντίστοιχα) τότε να αποδείξετε πως:

 αντιστρέφεται στον κύκλο
αντιστρέφεται στον κύκλο 
 αντιστρέφεται στον κύκλο
αντιστρέφεται στον κύκλο 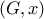
 αντιστρέφεται στον κύκλο
αντιστρέφεται στον κύκλο 
 αντιστρέφεται σε κύκλο που διέρχεται από τα
αντιστρέφεται σε κύκλο που διέρχεται από τα  (αντίστροφα των
(αντίστροφα των  ) κι έχει ακτίνα
) κι έχει ακτίνα 


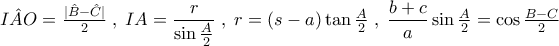 και
και 
 είναι:
είναι:
![R^2+\dfrac{2Rr^2}{2R\sin^2\frac{A}{2}}-2Rr\dfrac{\cos\frac{B-C}{2}}{\sin\frac{A}{2}} = R^2-2Rr\left[\dfrac{\cos\frac{B-C}{2}}{\sin\frac{A}{2}}-\dfrac{r}{2R\sin^2\frac{A}{2}}\right] = R^2+\dfrac{2Rr^2}{2R\sin^2\frac{A}{2}}-2Rr\dfrac{\cos\frac{B-C}{2}}{\sin\frac{A}{2}} = R^2-2Rr\left[\dfrac{\cos\frac{B-C}{2}}{\sin\frac{A}{2}}-\dfrac{r}{2R\sin^2\frac{A}{2}}\right] =](/forum/ext/geomar/texintegr/latexrender/pictures/bfbcd7c8905f09db2c3569da787bd5c6.png)
![R^2-2Rr\left[\dfrac{b+c}{a}-1-\dfrac{(s-a)\tan\frac{A}{2}}{2R\sin^2\frac{A}{2}}+1\right] = R^2-2Rr\left[\dfrac{b+c-a}{a}-\dfrac{s-a}{2R\sin\frac{A}{2}\cos\frac{A}{2}}+1\right] = R^2-2Rr\left[\dfrac{b+c}{a}-1-\dfrac{(s-a)\tan\frac{A}{2}}{2R\sin^2\frac{A}{2}}+1\right] = R^2-2Rr\left[\dfrac{b+c-a}{a}-\dfrac{s-a}{2R\sin\frac{A}{2}\cos\frac{A}{2}}+1\right] =](/forum/ext/geomar/texintegr/latexrender/pictures/2a9562fc6da2364ecb96a7c8201e0d8c.png)
![R^2-2Rr\left[\dfrac{2(s-a)}{a}-\dfrac{2(s-a)}{2R\sin A}+1\right] = R^2-2Rr\left[\dfrac{2(s-a)}{a}-\dfrac{2(s-a)}{a}+1\right] = R^2-2Rr\left[\dfrac{2(s-a)}{a}-\dfrac{2(s-a)}{2R\sin A}+1\right] = R^2-2Rr\left[\dfrac{2(s-a)}{a}-\dfrac{2(s-a)}{a}+1\right] =](/forum/ext/geomar/texintegr/latexrender/pictures/a6b3615c6270f98d0923cf508093e796.png)
