ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 36: Θεωρούμε τους πενταψήφιους αριθμούςκαι
. Αν
, να βρεθεί ο αριθμός
(Πηγή: ΜΑΘΗΜΑΤΙΚΕΣ ΟΛΥΜΠΙΑΔΕΣ για Δημοτικό και Γυμνάσιο, των Σ. Λουρίδα και Κ. Σάλαρη)
Ο αριθμός PR5T είναι ο

Συντονιστής: ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 36: Θεωρούμε τους πενταψήφιους αριθμούςκαι
. Αν
, να βρεθεί ο αριθμός
(Πηγή: ΜΑΘΗΜΑΤΙΚΕΣ ΟΛΥΜΠΙΑΔΕΣ για Δημοτικό και Γυμνάσιο, των Σ. Λουρίδα και Κ. Σάλαρη)

 ώστε να ισχύει η αριθμητική ισότητα
ώστε να ισχύει η αριθμητική ισότηταΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 37: Να τοποθετήσετε παρενθέσεις στο αριστερό σκέλος της ισότητας:ώστε να ισχύει η αριθμητική ισότητα
(ΠΗΓΗ: ίδια με αυτήν της άσκησης 36)

 χρόνια μεγαλύτερη από την Άννα. Η Ιωάννα είναι τρία χρόνια μεγαλύτερη από την Βαρβάρα.
χρόνια μεγαλύτερη από την Άννα. Η Ιωάννα είναι τρία χρόνια μεγαλύτερη από την Βαρβάρα. Καλησπέρα.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 38: (Μια ακόμα από το βιβλίο του εξαιρετικού φίλου Σωτήρη Λουρίδα: ΜΑΘΗΜΑΤΙΚΕΣ ΟΛΥΜΠΙΑΔΕΣ για μαθητές Δημοτικού και Γυμνασίου):
Η Άννα έχει τρεις μεγαλύτερες αδελφές. Η Βαρβάρα είναιχρόνια μεγαλύτερη από την Άννα. Η Ιωάννα είναι τρία χρόνια μεγαλύτερη από την Βαρβάρα.
Η Μαρία είναι τέσσερα χρόνια μεγαλύτερη από την Ιωάννα. Η Μαρία έχει διπλάσια ηλικία από την Βαρβάρα. Πόσων χρονών είναι η Άννα;
 την Άννα
την Άννα  την Βαρβάρα
την Βαρβάρα την Ιωάννα
την Ιωάννα  την Μαρία
την Μαρία




 χρονών.
χρονών. υπάρχουν ανάμεσα στους αριθμούς
υπάρχουν ανάμεσα στους αριθμούς  και
και 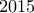
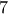 υπάρχουν ανάμεσα στους αριθμούς
υπάρχουν ανάμεσα στους αριθμούς  και
και 
ΚαλησπέραΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 39: Να βρείτε: (α) Πόσα πολλαπλάσια τουυπάρχουν ανάμεσα στους αριθμούς
και
(β) Πόσα πολλαπλάσια τουυπάρχουν ανάμεσα στους αριθμούς
και
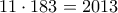 άρα ανάμεσα στο
άρα ανάμεσα στο  και στο
και στο  μπορούμε να πούμε ότι θα υπάρχουν
μπορούμε να πούμε ότι θα υπάρχουν  πολ/σια του
πολ/σια του 
 και
και  άρα ανάμεσα στο
άρα ανάμεσα στο  και
και 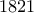 υπάρχουν
υπάρχουν  πολ/σια του
πολ/σια του 
 και όχι
και όχι 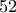 ευχαριστώ πολύ τον κύριο Δημήτρη για την επισήμανση.
ευχαριστώ πολύ τον κύριο Δημήτρη για την επισήμανση. , αν γνωρίζουμε ότι ο αριθμός
, αν γνωρίζουμε ότι ο αριθμός  διαιρείται με τον αριθμό
διαιρείται με τον αριθμό 
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 40: Να βρεθούν όλες οι τιμές του φυσικού αριθμού, αν γνωρίζουμε ότι ο αριθμός
διαιρείται με τον αριθμό
 να διαιρείται ακριβώς με τον αριθμό
να διαιρείται ακριβώς με τον αριθμό  Δηλαδή
Δηλαδή 
 να είναι ακέραιος.Δηλαδή
να είναι ακέραιος.Δηλαδή  Δηλαδή
Δηλαδή 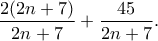
 Τώρα θα πρέπει να βρούμε πότε ο αριθμός
Τώρα θα πρέπει να βρούμε πότε ο αριθμός  είναι ακέραιος...Οι διαιρέτες του
είναι ακέραιος...Οι διαιρέτες του  είναι οι:
είναι οι: Όμως θέλουμε να είναι αριθμοί μεγαλύτεροι του
Όμως θέλουμε να είναι αριθμοί μεγαλύτεροι του 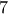 ώστε να μπορούμε να αφαιρέσουμε από αυτούς το
ώστε να μπορούμε να αφαιρέσουμε από αυτούς το 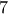 και το αποτέλεσμα να το διαιρέσουμε με το
και το αποτέλεσμα να το διαιρέσουμε με το  για να ισχύει
για να ισχύει  Oι αριθμοί που απομένουν είναι οι:
Oι αριθμοί που απομένουν είναι οι: Αφαιρούμε το
Αφαιρούμε το  και διαιρούμε τα αποτελέσματα με το
και διαιρούμε τα αποτελέσματα με το  Έτσι οι τιμές που μπορεί να πάρει ο n είναι:
Έτσι οι τιμές που μπορεί να πάρει ο n είναι:
 , όπου
, όπου  είναι φυσικοί αριθμοί. (
είναι φυσικοί αριθμοί. ( )
) είναι άρτιος ή περιττός.
είναι άρτιος ή περιττός. , να δείξετε ότι ο
, να δείξετε ότι ο  είναι τέλειος.
είναι τέλειος.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 41: Θεωρούμε τον αριθμό, όπου
είναι φυσικοί αριθμοί.
(α) Να εξετάσετε αν ο αριθμόςείναι άρτιος ή περιττός.
(β) Ένας αριθμός λέγεται τέλειος, όταν είναι ίσος με το άθροισμα των γνήσιων θετικών διαιρετών του. Αν, να δείξετε ότι ο
είναι τέλειος.
(ΣΗΜ: Γνήσιοι διαιρέτες ενός αριθμού λέγονται όλοι οι διαιρέτες του εκτός από τον εαυτό του)
 =άρτιος+περιττός+περιττός=2.m+2.n+1+2.k+1=2.(m+n+k)+2=άρτιος
=άρτιος+περιττός+περιττός=2.m+2.n+1+2.k+1=2.(m+n+k)+2=άρτιος Γνήσιοι διαιρέτες
Γνήσιοι διαιρέτες  και
και  .Άρα ο αριθμός Α είναι τέλειος....
.Άρα ο αριθμός Α είναι τέλειος....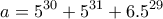 .
. διαιρείται με το
διαιρείται με το  και με το
και με το 

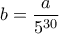 δεν είναι ακέραιος
δεν είναι ακέραιος , ώστε ο αριθμός
, ώστε ο αριθμός 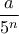 να είναι φυσικός, αλλά όχι τέλειο τετράγωνο.
να είναι φυσικός, αλλά όχι τέλειο τετράγωνο.Καλησπέρα κύριε ΔημήτρηΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 42: Δίνεται ο αριθμός.
(α) Να αποδείξετε ότι οδιαιρείται με το
και με το
(β) Να βρείτε τα δύο τελευταία ψηφία του
(γ) Να δείξετε ότι ο αριθμόςδεν είναι ακέραιος
(δ) Να βρείτε την μέγιστη τιμή του φυσικού αριθμού, ώστε ο αριθμός
να είναι φυσικός, αλλά όχι τέλειο τετράγωνο.



 τελειώνει σε
τελειώνει σε 
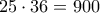

 ο οποίος δεν είναι ακέραιος.
ο οποίος δεν είναι ακέραιος.
 δεν διαιρείται με το
δεν διαιρείται με το  πρέπει
πρέπει 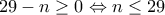
 δεν ικανοποιούνται οι συνθήκες.
δεν ικανοποιούνται οι συνθήκες.
 ο οποίος είναι ακέραιος και δεν είναι τέλειο τετράγωνο.
ο οποίος είναι ακέραιος και δεν είναι τέλειο τετράγωνο.
 , όπου
, όπου  . (Φυσικά, αν η βάση της δύναμης λήγει σε
. (Φυσικά, αν η βάση της δύναμης λήγει σε  ή
ή  ή
ή  ή
ή  , τότε και ο δοσμένος αριθμός θα λήγει επίσης σε
, τότε και ο δοσμένος αριθμός θα λήγει επίσης σε  ή
ή  ή
ή  ή
ή  αντιστοίχως, οπότε η απάντηση είναι άμεση). Αυτό το πετυχαίνουμε κάνοντας την διαίρεση του εκθέτη με το
αντιστοίχως, οπότε η απάντηση είναι άμεση). Αυτό το πετυχαίνουμε κάνοντας την διαίρεση του εκθέτη με το  . Εύκολα μπορούμε να διαπιστώσουμε ότι ο αριθμός
. Εύκολα μπορούμε να διαπιστώσουμε ότι ο αριθμός  , θα λήγει πάντα ή σε
, θα λήγει πάντα ή σε  , ή σε
, ή σε  , ή σε
, ή σε  ,ή σε
,ή σε  . Επίσης εύκολα διαπιστώνουμε ότι αν ένας αριθμός
. Επίσης εύκολα διαπιστώνουμε ότι αν ένας αριθμός  λήγει σε
λήγει σε  ή
ή  ή
ή  ή
ή  , τότε και ο
, τότε και ο 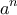 , θα λήγει επίσης σε
, θα λήγει επίσης σε  ή
ή  ή
ή  ή
ή  αντιστοίχως. Για παράδειγμα, για να βρούμε το ψηφίο των μονάδων του αριθμού
αντιστοίχως. Για παράδειγμα, για να βρούμε το ψηφίο των μονάδων του αριθμού  , εργαζόμαστε ως εξής: Κάνουμε την διαίρεση του
, εργαζόμαστε ως εξής: Κάνουμε την διαίρεση του  με το
με το  και βρίσκουμε πηλίκο το
και βρίσκουμε πηλίκο το  και υπόλοιπο το
και υπόλοιπο το  . Άρα μπορούμε να γράψουμε
. Άρα μπορούμε να γράψουμε . Άρα έχουμε:
. Άρα έχουμε: . 'Ομως ο
. 'Ομως ο  θα λήγει όπου και ο
θα λήγει όπου και ο  , δηλαδή σε
, δηλαδή σε  . Άρα και ο
. Άρα και ο  θα λήγει επίσης σε
θα λήγει επίσης σε  . Και επομένως ο
. Και επομένως ο 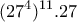 , θα λήγει σε
, θα λήγει σε 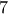 . Δηλαδή το ψηφίο των μονάδων του
. Δηλαδή το ψηφίο των μονάδων του  είναι το
είναι το 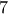 .
. και στη συνέχεια να εξετάσετε αν ο αριθμός αυτός διαιρείται
και στη συνέχεια να εξετάσετε αν ο αριθμός αυτός διαιρείται .
.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 43: Μπορούμε εύκολα να βρούμε το ψηφίο των μονάδων ενός φυσικού αριθμού που είναι γραμμένος στην μορφή δύναμης. Ένας τρόπος είναι να γράψουμε τον εκθέτη στην μορφή, όπου
. (Φυσικά, αν η βάση της δύναμης λήγει σε
ή
ή
ή
, τότε και ο δοσμένος αριθμός θα λήγει επίσης σε
ή
ή
ή
αντιστοίχως, οπότε η απάντηση είναι άμεση). Αυτό το πετυχαίνουμε κάνοντας την διαίρεση του εκθέτη με το
. Εύκολα μπορούμε να διαπιστώσουμε ότι ο αριθμός
, θα λήγει πάντα ή σε
, ή σε
, ή σε
,ή σε
. Επίσης εύκολα διαπιστώνουμε ότι αν ένας αριθμός
λήγει σε
ή
ή
ή
, τότε και ο
, θα λήγει επίσης σε
ή
ή
ή
αντιστοίχως. Για παράδειγμα, για να βρούμε το ψηφίο των μονάδων του αριθμού
, εργαζόμαστε ως εξής: Κάνουμε την διαίρεση του
με το
και βρίσκουμε πηλίκο το
και υπόλοιπο το
. Άρα μπορούμε να γράψουμε
ότι. Άρα έχουμε:
. 'Ομως ο
θα λήγει όπου και ο
, δηλαδή σε
. Άρα και ο
θα λήγει επίσης σε
. Και επομένως ο
, θα λήγει σε
. Δηλαδή το ψηφίο των μονάδων του
είναι το
.
Με βάση τα παραπάνω, να βρείτε το ψηφίο των μονάδων του αριθμού:και στη συνέχεια να εξετάσετε αν ο αριθμός αυτός διαιρείται
με το.
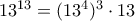 άρα ο αριθμός λήγει σε
άρα ο αριθμός λήγει σε 
 ο αριθμός λήγει σε
ο αριθμός λήγει σε 
 λήγει σε
λήγει σε  άρα σε
άρα σε 


(α)ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 44: Δίνεται ο αριθμός

(α) Να εξετάσετε αν είναι πρώτος
(β) Να αποδείξετε ότι
ΣΗΜ: Διόρθωσα μια απροσεξία στο (β) ερώτημα




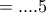
Ωραία maria.p . Να συμπληρώσω μόνο ότι αντί να γράψουμεmaria.p έγραψε:(α)ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 44: Δίνεται ο αριθμός

(α) Να εξετάσετε αν είναι πρώτος
(β) Να αποδείξετε ότι
ΣΗΜ: Διόρθωσα μια απροσεξία στο (β) ερώτημα
Ο αριθμος α τελειωνει σε 5 και διαιρειται με το 5.Αρα ο αριθμος α δεν ειναι πρωτος
 , πρέπει να γράψουμε ότι:
, πρέπει να γράψουμε ότι: λήγει σε
λήγει σε  ,
,  λήγει σε
λήγει σε  ,
, λήγει σε
λήγει σε  , άρα ο
, άρα ο  , θα λήγει σε
, θα λήγει σε 
 , είναι ο εξής:
, είναι ο εξής: 
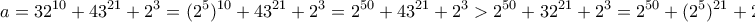
 και άρα
και άρα 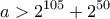
 % της τροφής που υπάρχει στην ταϊστρα του. Αν βάλουμε μέσα στην ταϊστρα
% της τροφής που υπάρχει στην ταϊστρα του. Αν βάλουμε μέσα στην ταϊστρα Ωραία,ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 45: Ένα παράξενο ζώο τρώει κάθε μέρα το% της τροφής που υπάρχει στην ταϊστρα του. Αν βάλουμε μέσα στην ταϊστρα
4 κιλά τροφής, πόσα κιλά θα απομείνουν μετά από τρεις μέρες;
 κιλά και θα απομείνουν
κιλά και θα απομείνουν 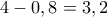 κιλά
κιλά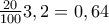 κιλά και θα απομείνουν
κιλά και θα απομείνουν 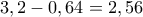 κιλά
κιλά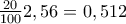 κιλά και θα απομείνουν
κιλά και θα απομείνουν κιλά
κιλάΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες