1)

2)

3)
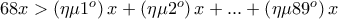
Συντονιστής: Παύλος Μαραγκουδάκης


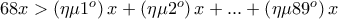
 . (1)
. (1)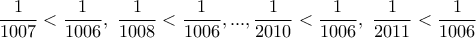 .
. ), έχουμε :
), έχουμε : . Αν προσθέσουμε στα δύο μέλη το
. Αν προσθέσουμε στα δύο μέλη το  , έχουμε:
, έχουμε: δηλαδή :
δηλαδή : .
. , τότε ισχύει :
, τότε ισχύει :  άρα
άρα  .
.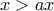


 έχουμε :
έχουμε :  .
. (1)
(1) , ισχύουν :
, ισχύουν : και
και  .
. φορές το
φορές το  και
και  φορές το
φορές το  ) :
) : . Δηλαδή, αν ονομάσουμε
. Δηλαδή, αν ονομάσουμε 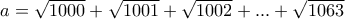 , ισχύει :
, ισχύει :  άρα
άρα  .
.


 , έχουμε :
, έχουμε : 
 (1)
(1) έχουμε :
έχουμε : (
( σχέσεις)
σχέσεις) (
( σχέσεις)
σχέσεις) (
( σχέσεις)
σχέσεις) (
( σχέσεις).
σχέσεις).
 άρα
άρα  . Eπομένως, η προηγούμενη ανισότητα γίνεται :
. Eπομένως, η προηγούμενη ανισότητα γίνεται : . Αν ονομάσουμε
. Αν ονομάσουμε  , έχουμε
, έχουμε άρα
άρα  .
.


 , έχουμε :
, έχουμε :  .
. Μιας και μας έδειξες τον δρόμο Γιώργο:Παύλος Μαραγκουδάκης έγραψε:Να λυθούν οι ανισώσεις:
3)










 . Δηλαδή,
. Δηλαδή, 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες