Απλά, ορίζουμεΜπάμπης Στεργίου έγραψε:αλλά θα ήθελα και την άποψή σας
 και το πρόβλημα σταματά να υφίσταται. Το έχω ξαναπεί και εδώ.
και το πρόβλημα σταματά να υφίσταται. Το έχω ξαναπεί και εδώ.Συντονιστής: Γιώργος Ρίζος
Απλά, ορίζουμεΜπάμπης Στεργίου έγραψε:αλλά θα ήθελα και την άποψή σας
 και το πρόβλημα σταματά να υφίσταται. Το έχω ξαναπεί και εδώ.
και το πρόβλημα σταματά να υφίσταται. Το έχω ξαναπεί και εδώ.ΔΗΜΗΤΡΗΣ έγραψε:Καλησπέρα.tsaknakis έγραψε:Δεν υπάρχει λόγος να περιορίσουμε τη διαίρεση μόνο με σταθερά μονώνυμα. αν για παράδειγμα ορίσουμε ως πηλίκο της διαίρεσης ενος μονωνύμουμε ένα μονώνυμο
να είναι το μονώνυμο
(αν φυσικά υπάρχει) τέτοιο ώστε
, δεν υπάρχει πρόβλημα να γράψεις τη διαίρεση
Δεν περιορίζουμε την διαίρεση μόνο με σταθερά μονώνυμα. ΄Μπορούμε φυσικά να έχουμε διαίρεση μονωνύμου διά μονώνυμο, αλλά το αποτέλεσμα της διαίρεσης δεν θα είναι μονώνυμο (με βάση αυτά που έγραψε ο Αντώνης λίγο πιο πάνω),(εκτός αν ο παρονομαστής είναι το μη μηδενικό σταθερό μονώνυμο)
΄
 αν και μόνο αν
αν και μόνο αν 
 αφού
αφού  )
) δεν είναι μονώνυμο,αλλά ότι η αλγεβρική παράσταση
δεν είναι μονώνυμο,αλλά ότι η αλγεβρική παράσταση 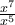 δεν είναι μονώνυμο.
δεν είναι μονώνυμο. ορίζεται για κάθε τιμη του
ορίζεται για κάθε τιμη του 
 ορίζεται για
ορίζεται για 
Αν ερμηνεύω σωστά (που μάλλον όχι ) το οποιοδήποτε στοιχείο τουΤοείναι μάλιστα μεταθετικός δακτύλιος οπότε με την ίδια διαδικασία μπορούμε να ορίσουμε το
και ομοίως πολυωνυμικούς δακτύλιους περισσοτέρων μεταβλητών. Ένα στοιχείο του
ονομάζεται μονώνυμο αν μπορεί να γραφτεί στην μορφή μετα απο πραξεις
για κάποιο
και κάποια
.
![R[x_1,\ldots,x_n] R[x_1,\ldots,x_n]](/forum/ext/geomar/texintegr/latexrender/pictures/d1dd685fa457a5500081458f5cdf2d27.png) μπορεί να γραφτεί σαν
μπορεί να γραφτεί σαν  για κάποιο
για κάποιο  και κάποια
και κάποια  είναι μονώνυμο .
είναι μονώνυμο . , μάλλον δεν κατάλαβα καλά, έχω και χρόνια να ασχοληθώ με αυτά .
, μάλλον δεν κατάλαβα καλά, έχω και χρόνια να ασχοληθώ με αυτά .Υπάρχει διάφορα στο τη εκφράζουν τα μονώνυμα και σε ποιες πράξεις γίνονται με αυτά .Μιχάλης Νάννος έγραψε:Καλησπέρα σας. Θα συμφωνήσω απολύτως με το Δημήτρη ότι θα πρέπει να ξέρουμε ποια σύμβαση ακολουθούμε (κάτι ανάλογο με την προτεραιότητα των πράξεων, π.χκαι όχι
).
Με τη λογική του Κώστα (στην ουσία του ορισμού) η έκφρασηΤηλέγραφος Κώστας έγραψε:Τα μονώνυμα εκφράζουν πολλαπλασιασμό μεταξύ των μεταβλητών και όχι διαίρεση η άλλη πράξη.
Η παράστασηέχει την διαίρεση (
)οπότε δεν είναι μονώνυμο.
δεν είναι μονώνυμο, γιατί μεταξύ των μεταβλητών παρεμβάλλεται η πρόσθεση και όχι ο πολλαπλασιασμός, ενώ σύμφωνα με την Πανεπιστημιακή αφηρημένη Άλγεβρα, όπως τεκμηριώνει πιο πάνω ο Δημήτρης, είναι μονώνυμο.
Μην ξεχνάμε τις ασκήσεις του τύπου: Να βρεθούν οι φυσικοί αριθμοί, ώστε η αλγεβρική παράσταση
να είναι μονώνυμο… προϋποθέτει η άσκηση λοιπόν, πως οι δύο όροι θα προστεθούν μεταξύ τους (εξισώνοντας τους αντίστοιχους εκθέτες για να εξασφαλίσουμε ίσα κύρια μέρη) και θα μείνει ένας.
Άρα μελετάμε, αν είναι μονώνυμο, μια έκφραση όπως μας δίνεται ή όπως θα διαμορφωθεί μετά από πράξεις – αναγωγές κ.λ.π;

Κώστα σωστά κατάλαβες. Πρώτα ορίζεται το πολυώνυμο και μετά το μονώνυμο. Με αυτήν την προσέγγιση, το γεγονός ότι κάθε πολυώνυμο μπορεί να γραφτεί σαν άθροισμα μονωνύμων είναι πλέον θεώρημα που πρέπει να αποδειχθεί.Τηλέγραφος Κώστας έγραψε:Δημήτρη: Στον παρακάτω ορισμό το κόκκινο δεν μου αρέσει , βέβαια δεν υποστηρίζω ότι είναι λάθος .Αν ερμηνεύω σωστά (που μάλλον όχι ) το οποιοδήποτε στοιχείο τουΤοείναι μάλιστα μεταθετικός δακτύλιος οπότε με την ίδια διαδικασία μπορούμε να ορίσουμε το
και ομοίως πολυωνυμικούς δακτύλιους περισσοτέρων μεταβλητών. Ένα στοιχείο του
ονομάζεται μονώνυμο αν μπορεί να γραφτεί στην μορφή μετα απο πραξεις
για κάποιο
και κάποια
.
μπορεί να γραφτεί σαν
για κάποιο
και κάποια
είναι μονώνυμο .
Αν είναι έτσι ο ορισμός του μονωνύμου έρχεται μετά τον ορισμού του πολυωνύμου, μάλλον δεν κατάλαβα καλά, έχω και χρόνια να ασχοληθώ με αυτά .
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες