 .
.Τραπέζιο που γέρνει
Συντονιστής: Γιώργος Ρίζος
Re: Τραπέζιο που γέρνει
Από Π.Θ σταKARKAR έγραψε:Υπολογίστε το εμβαδόν του τετραπλεύρου.
 και
και  παίρνουμε αντίστοιχα τις σχέσεις:
παίρνουμε αντίστοιχα τις σχέσεις:

Ακόμα, ισχύει:

Αντικαθιστώντας την παραπάνω στην
 είναι:
είναι:
Λόγω της
 όμως η τελευταία γίνεται:
όμως η τελευταία γίνεται:
Αντικαθιστώντας στην
 έχουμε:
έχουμε:
Εύκολα τώρα, από τον τύπο του εμβαδού τραπεζίου έχουμε:

Επομένως, το ζητούμενο βρέθηκε.
Πάντα κατ' αριθμόν γίγνονται... ~ Πυθαγόρας
Ψυρούκης Ραφαήλ
Ψυρούκης Ραφαήλ
- Μιχάλης Νάννος
- Επιμελητής
- Δημοσιεύσεις: 3549
- Εγγραφή: Δευ Ιαν 05, 2009 4:09 pm
- Τοποθεσία: Σαλαμίνα
- Επικοινωνία:
Re: Τραπέζιο που γέρνει
Καλημέρα σας. Αν φέρουμεKARKAR έγραψε:Υπολογίστε το εμβαδόν του τετραπλεύρου.
 , τότε από τον τύπο του Ήρωνα (
, τότε από τον τύπο του Ήρωνα ( ημιπερίμετρος) παίρνουμε
ημιπερίμετρος) παίρνουμε  και
και 
«Δε θα αντικαταστήσει ο υπολογιστής τον καθηγητή...θα αντικατασταθεί ο καθηγητής που δεν ξέρει υπολογιστή...» - Arthur Clarke
Re: Τραπέζιο που γέρνει
Προφανώς στη Σαλαμίνα οι μαθητές διδάσκονται τον τύπο του Ήρωνα στο Γυμνάσιο  ( Καλημέρα Μιχάλη ! )
( Καλημέρα Μιχάλη ! )
- Μιχάλης Νάννος
- Επιμελητής
- Δημοσιεύσεις: 3549
- Εγγραφή: Δευ Ιαν 05, 2009 4:09 pm
- Τοποθεσία: Σαλαμίνα
- Επικοινωνία:
Re: Τραπέζιο που γέρνει
Το καλύτερο το είπε τηλεφωνικά ο Κώστας ο Βήττας...Μιχάλη, στη Σαλαμίνα οι μαθητές Γυμνασίου κάνουν συζυγή αρμονικά; 
Καλημέρα και πάλι.
Καλημέρα και πάλι.
«Δε θα αντικαταστήσει ο υπολογιστής τον καθηγητή...θα αντικατασταθεί ο καθηγητής που δεν ξέρει υπολογιστή...» - Arthur Clarke
- vittasko
- Επιμελητής
- Δημοσιεύσεις: 2230
- Εγγραφή: Πέμ Ιαν 08, 2009 8:46 am
- Τοποθεσία: Μαρούσι - Αθήνα.
- Επικοινωνία:
Re: Τραπέζιο που γέρνει
Στο σχήμα του Μιχάλη πιο πάνω, ας είναι  η προβολή του
η προβολή του  επί της
επί της  και έστω
και έστω 
Από το ορθογώνιο τρίγωνο , σύμφωνα με το Πυθαγόρειο θεώρημα, έχουμε
, σύμφωνα με το Πυθαγόρειο θεώρημα, έχουμε 
Ομοίως, από το ορθογώνιο τρίγωνο , έχουμε
, έχουμε 
Από με αφαίρεση κατά μέλη, έχουμε
με αφαίρεση κατά μέλη, έχουμε 


Από με πράξεις προκύπτει
με πράξεις προκύπτει 
Εύκολα τώρα, από το ορθογώνιο τρίγωνο υπολογίζουμε το
υπολογίζουμε το  το οποίο ταυτίζεται με το ύψος του δοσμένου τραπεζίου
το οποίο ταυτίζεται με το ύψος του δοσμένου τραπεζίου 
Πράγματι, ισχύει


Από και
και  και
και 

 και το ζητούμενο έχει υπολογιστεί.
και το ζητούμενο έχει υπολογιστεί.
Κώστας Βήττας.
 η προβολή του
η προβολή του  επί της
επί της  και έστω
και έστω 
Από το ορθογώνιο τρίγωνο
 , σύμφωνα με το Πυθαγόρειο θεώρημα, έχουμε
, σύμφωνα με το Πυθαγόρειο θεώρημα, έχουμε 
Ομοίως, από το ορθογώνιο τρίγωνο
 , έχουμε
, έχουμε 
Από
 με αφαίρεση κατά μέλη, έχουμε
με αφαίρεση κατά μέλη, έχουμε 


Από
 με πράξεις προκύπτει
με πράξεις προκύπτει 
Εύκολα τώρα, από το ορθογώνιο τρίγωνο
 υπολογίζουμε το
υπολογίζουμε το  το οποίο ταυτίζεται με το ύψος του δοσμένου τραπεζίου
το οποίο ταυτίζεται με το ύψος του δοσμένου τραπεζίου 
Πράγματι, ισχύει



Από
 και
και  και
και 

 και το ζητούμενο έχει υπολογιστεί.
και το ζητούμενο έχει υπολογιστεί.Κώστας Βήττας.
Re: Τραπέζιο που γέρνει
Και μια εφαρμογή των ομοίων τριγώνων μαζί με τον ξεχασμένο Ήρωνα.KARKAR έγραψε:Υπολογίστε το εμβαδόν του τετραπλεύρου.
Θεωρούμε τις προεκτάσεις των
 οι οποίες ορίζουν το σημείο
οι οποίες ορίζουν το σημείο  .
.Αν θέσουμε τις
 και
και  τότε από την ομοιότητα των τριγώνων
τότε από την ομοιότητα των τριγώνων 
και όπως φαίνεται από τις πράξεις στο ανωτέρω σχήμα θα είναι:

Εφαρμόζοντας τον τύπο του Ήρωνα:

στα δύο αυτά τρίγωνα βρίσκουμε:
 και
και 
Επομένως η διαφορά αυτών δίνει:

Οι πράξεις με τον τύπο του Ήρωνα έγιναν απ' ευθείας από το CAS του Geogebra.
Κώστας Δόρτσιος
- Ηλιας Φραγκάκος
- Δημοσιεύσεις: 512
- Εγγραφή: Παρ Σεπ 13, 2013 11:40 pm
- Τοποθεσία: Χανιά Κρήτης
- Επικοινωνία:
Re: Τραπέζιο που γέρνει
Στο τρ.  η υποτείνουσα είναι
η υποτείνουσα είναι  άρα το άθροισμα των τετραγώνων των δύο καθέτων είναι
άρα το άθροισμα των τετραγώνων των δύο καθέτων είναι 
Στο τρ.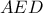 η υποτείνουσα είναι
η υποτείνουσα είναι  , άρα το άθροισμα των τετραγώνων των καθέτων είναι
, άρα το άθροισμα των τετραγώνων των καθέτων είναι  .
.
Τα τρίγ. έχουν κοινό ύψος, οπότε η διαφορά του από το
από το 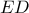 είναι
είναι  . Η διαφορά των τετραγώνων δύο διαδοχικών είναι ίση με το διπλάσιο του μικρότερου συν
. Η διαφορά των τετραγώνων δύο διαδοχικών είναι ίση με το διπλάσιο του μικρότερου συν  , άρα περιττός αριθμός. Οπότε η διαφορά του
, άρα περιττός αριθμός. Οπότε η διαφορά του  από το
από το 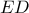 είναι ζυγός. Παίρνουμε λοιπόν την περίπτωση να είναι
είναι ζυγός. Παίρνουμε λοιπόν την περίπτωση να είναι  .
.
Άρα έχουμε δύο άσσους και . Συνεπάγεται,
. Συνεπάγεται,  .
.
Άρα το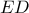 είναι
είναι  . Συμπεραίνουμε λοιπόν ότι το τετράγωνο του ύψους του τριγώνου και του τραπεζίου είναι
. Συμπεραίνουμε λοιπόν ότι το τετράγωνο του ύψους του τριγώνου και του τραπεζίου είναι  . Άρα το ύψος του τραπεζίου είναι ρίζα
. Άρα το ύψος του τραπεζίου είναι ρίζα  , δηλαδή
, δηλαδή  . Αν κάποιος έμπειρος έχει να παρατηρήσει κάτι σε αυτή τη λύση, η παρατήρησή του είναι ευπρόσδεκτη και τον ευχαριστώ.
. Αν κάποιος έμπειρος έχει να παρατηρήσει κάτι σε αυτή τη λύση, η παρατήρησή του είναι ευπρόσδεκτη και τον ευχαριστώ.
 η υποτείνουσα είναι
η υποτείνουσα είναι  άρα το άθροισμα των τετραγώνων των δύο καθέτων είναι
άρα το άθροισμα των τετραγώνων των δύο καθέτων είναι 
Στο τρ.
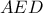 η υποτείνουσα είναι
η υποτείνουσα είναι  , άρα το άθροισμα των τετραγώνων των καθέτων είναι
, άρα το άθροισμα των τετραγώνων των καθέτων είναι  .
.Τα τρίγ. έχουν κοινό ύψος, οπότε η διαφορά του
 από το
από το 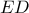 είναι
είναι  . Η διαφορά των τετραγώνων δύο διαδοχικών είναι ίση με το διπλάσιο του μικρότερου συν
. Η διαφορά των τετραγώνων δύο διαδοχικών είναι ίση με το διπλάσιο του μικρότερου συν  , άρα περιττός αριθμός. Οπότε η διαφορά του
, άρα περιττός αριθμός. Οπότε η διαφορά του  από το
από το 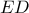 είναι ζυγός. Παίρνουμε λοιπόν την περίπτωση να είναι
είναι ζυγός. Παίρνουμε λοιπόν την περίπτωση να είναι  .
. Άρα έχουμε δύο άσσους και
 . Συνεπάγεται,
. Συνεπάγεται,  .
.Άρα το
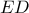 είναι
είναι  . Συμπεραίνουμε λοιπόν ότι το τετράγωνο του ύψους του τριγώνου και του τραπεζίου είναι
. Συμπεραίνουμε λοιπόν ότι το τετράγωνο του ύψους του τριγώνου και του τραπεζίου είναι  . Άρα το ύψος του τραπεζίου είναι ρίζα
. Άρα το ύψος του τραπεζίου είναι ρίζα  , δηλαδή
, δηλαδή  . Αν κάποιος έμπειρος έχει να παρατηρήσει κάτι σε αυτή τη λύση, η παρατήρησή του είναι ευπρόσδεκτη και τον ευχαριστώ.
. Αν κάποιος έμπειρος έχει να παρατηρήσει κάτι σε αυτή τη λύση, η παρατήρησή του είναι ευπρόσδεκτη και τον ευχαριστώ.- Συνημμένα
-
- png02012014.png (4.16 KiB) Προβλήθηκε 463 φορές
" Ή ταν, ή τα παρατάν " Είπε ο Λεωνίδας με τα λίγα Περσικά του και ίδρυσε το σύλλογο προς διάδοση της Ελληνοτουρκικής Φιλίας με το διακριτικό τίτλο "Νικηταράς ο Τουρκοφάγος"
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
