Ι. Εικασία Fermat (1601-1665)
Ο Fermat είχε ισχυρισθεί το 1640 ότι οι αριθμοί
 "αριθμοί Fermat" είναι πρώτοι αριθμοί (πλάνη Fermat).
"αριθμοί Fermat" είναι πρώτοι αριθμοί (πλάνη Fermat).Η εικασία Fermat ισχύει για τους αριθμούς
 .
.Το 1732 όμως, ο Euler απέδειξε ότι ο
 , δηλαδή γινόμενο 2 αριθμών, άρα σύνθετος αριθμός. Οι πρώτοι αριθμοί μέχρι το 641 είναι 116. Ο Fermat όμως δεν έκανε όλες αυτές τις διαιρέσεις σύμφωνα με την πρόταση Ερατοσθέση. Όπως μας πληροφόρησε ο "Demetres" στην ανάρτησή μου "Γρίφος Euler", ο Euler έκανε μόνο 4 δοκιμές, γιατί προηγουμένως είχε διατυπώσει κάποιο κριτήριο, που περιόριζε τον αριθμό των δοκιμών.
, δηλαδή γινόμενο 2 αριθμών, άρα σύνθετος αριθμός. Οι πρώτοι αριθμοί μέχρι το 641 είναι 116. Ο Fermat όμως δεν έκανε όλες αυτές τις διαιρέσεις σύμφωνα με την πρόταση Ερατοσθέση. Όπως μας πληροφόρησε ο "Demetres" στην ανάρτησή μου "Γρίφος Euler", ο Euler έκανε μόνο 4 δοκιμές, γιατί προηγουμένως είχε διατυπώσει κάποιο κριτήριο, που περιόριζε τον αριθμό των δοκιμών.Το 1880 απεδείχθη από τον Landry ότι και ο
 είναι σύνθετος και δέχεται ως διαιρέτη τον
είναι σύνθετος και δέχεται ως διαιρέτη τον  .
.Καθώς αυξάνεται το
 οι αριθμοί
οι αριθμοί  αυξάνονται αλματωδώς, γι' αυτό ακόμα και με την χρήση των computers είναι δύσκολος ο χαρακτηρισμός, αν ένας
αυξάνονται αλματωδώς, γι' αυτό ακόμα και με την χρήση των computers είναι δύσκολος ο χαρακτηρισμός, αν ένας  είναι πρώτος ή σύνθετος, εκτός των λίγων αρχικών
είναι πρώτος ή σύνθετος, εκτός των λίγων αρχικών  .
.ΙΙ. Θα αποδείξουμε αλγεβρικά ότι το

Είναι



Αλλά

Αντικαθιστώ στην (1) το
 με
με από (2) και έχω
από (2) και έχω 

(θέτω
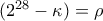 ) και
) και 
ΙΙΙ. Θεώρημα Gauss για τα κανονικά πολύγωνα
Ο Gauss, Γερμανός Μαθηματικός (1777-1855), σε ηλικία 18 ετών απέδειξε την πρόταση:
"Τα μόνα κανονικά πολύγωνα που μπορεί να κατασκευαστούν με κανόνα και διαβήτη είναι εκείνα των οποίων το πλήθος των πλευρών τους είναι της μορφής
 με
με  και
και  ή
ή 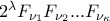 , όπου
, όπου  μη αρνητικός ακέραιος και
μη αρνητικός ακέραιος και  αριθμοί Fermat, πρώτοι και διαφορετικοί μεταξύ τους"
αριθμοί Fermat, πρώτοι και διαφορετικοί μεταξύ τους" Τέτοια είναι τα 3, 5, 17, 257, ... κλπ. Το 7/γωνο δεν κατασκευάζεται γιατί δεν είναι αριθμός Fermat. Ούτε το 9/γωνο γιατί είναι γινόμενο
 που δεν είναι διακεκριμένα.
που δεν είναι διακεκριμένα.Πηγές
1. Εισαγωγή στην Αριθμοθεωρία: Π. Μάγειρα 1964
2. Θεωρία Αριθμών: Κ. Λάκκη 1979
3. Μαθήματα επιπεδομετρίας: W. Servais-L.Jeronnez 1964, Μετάφραση: Ν. Σωτηράκη
