Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

ΗρακληςΕυαγγελινος · #1

1) Να δειχθεί ότι για $\alpha, \beta, \gamma \in R^+$ ισχύει:

$\frac{1}{\mid \alpha + \beta \mid} + \frac{1}{\mid \beta + \gamma \mid} + \frac{1}{\mid \gamma + \alpha \mid} \geq \frac{9}{2}\frac{1}{\mid \alpha \mid + \mid \beta \mid + \mid \gamma \mid}$

2) Αν $x_1, x_2, ..., x_{\nu} >0$ και $\kappa_1, \kappa_2, ..., \kappa_{\nu} \in N$ , να δειχθεί ότι:

$(\frac{\kappa_1x_1+\kappa_2x_2+...+\kappa_{\nu}x_{\nu}}{\kappa_1+\kappa_2+...+\kappa_{\nu}})^{\kappa_1+\kappa_2+\kappa_{\nu}} \geq x_1^{\kappa_1}x_2^{\kappa_2}...x_{\nu}^{\kappa_{\nu}}$

3) Να δειχθεί ότι: $3\nu(3\nu+1)^2>\sqrt[\nu]{1 \cdot 2 \cdot \cdot \cdot 3\nu}, \quad \nu \in N$

4) Αν $\alpha, \beta, \gamma \in R^{+}$ να αποδειχθεί ότι: $\frac{1}{(\alpha+\beta)\beta}+\frac{1}{(\beta+\gamma)\gamma}+\frac{1}{(\gamma+\alpha)\alpha} \geq \frac{9}{2(\alpha\beta+\beta\gamma+\gamma\alpha)}$

Ορέστης Λιγνός · #2

ΗρακληςΕυαγγελινος έγραψε:1) Να δειχθεί ότι για $\alpha, \beta, \gamma \in R^+$ ισχύει:

$\frac{1}{\mid \alpha + \beta \mid} + \frac{1}{\mid \beta + \gamma \mid} + \frac{1}{\mid \gamma + \alpha \mid} \geq \frac{9}{2}\frac{1}{\mid \alpha \mid + \mid \beta \mid + \mid \gamma \mid}$

Οι

είναι θετικοί, άρα η ανισότητα γίνεται $\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a} \geqslant \dfrac{9}{2(a+b+c)}$ , που είναι άμεση από AM-HM.

JimNt. · #3

ΗρακληςΕυαγγελινος έγραψε: 2) Αν $x_1, x_2, ..., x_{\nu} >0$ και $\kappa_1, \kappa_2, ..., \kappa_{\nu} \in N$ , να δειχθεί ότι:

$(\frac{\kappa_1x_1+\kappa_2x_2+...+\kappa_{\nu}x_{\nu}}{\kappa_1+\kappa_2+...+\kappa_{\nu}})^{\kappa_1+\kappa_2+\kappa_{\nu}} \geq x_1^{\kappa_1}x_2^{\kappa_2}...x_{\nu}^{\kappa_{\nu}}$

Άμεση από την Weighted AM-GM

. (Υποθέτουμε ότι εκθέτης είναι k_1+k_2+...+k_n

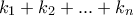, οι οποίοι δεν χρειάζεται να είναι φυσικοί)

harrisp · #4

Καλημέρα Ορέστη και Jim Nt.

Πολυ Χαλαρή η 3) Απο ΑΜ-ΓΜ αρκεί να αποδείξουμε οτι $RHS>\dfrac {3n+1}{2}$ που είναι προφανές

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #5

Ορέστης Λιγνός έγραψε:
ΗρακληςΕυαγγελινος έγραψε:1) Να δειχθεί ότι για $\alpha, \beta, \gamma \in R^+$ ισχύει:

$\frac{1}{\mid \alpha + \beta \mid} + \frac{1}{\mid \beta + \gamma \mid} + \frac{1}{\mid \gamma + \alpha \mid} \geq \frac{9}{2}\frac{1}{\mid \alpha \mid + \mid \beta \mid + \mid \gamma \mid}$
Οι είναι θετικοί, άρα η ανισότητα γίνεται $\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a} \geqslant \dfrac{9}{2(a+b+c)}$ , που είναι άμεση από AM-HM.

Ισχύει ακόμα και αν $a,b,c\in \mathbb{R}$

με $(a+b)(b+c)(c+a)\neq 0$

Διονύσιος Αδαμόπουλος · #6

ΗρακληςΕυαγγελινος έγραψε:
2) Αν $x_1, x_2, ..., x_{\nu} >0$ και $\kappa_1, \kappa_2, ..., \kappa_{\nu} \in N$ , να δειχθεί ότι:

$(\dfrac{\kappa_1x_1+\kappa_2x_2+...+\kappa_{\nu}x_{\nu}}{\kappa_1+\kappa_2+...+\kappa_{\nu}})^{\kappa_1+\kappa_2+...+\kappa_{\nu}} \geq x_1^{\kappa_1}x_2^{\kappa_2}...x_{\nu}^{\kappa_{\nu}}$

Ας λογαριθμήσουμε την ανισότητα.

Αρκεί:

$\ln[(\dfrac{\kappa_1x_1+\kappa_2x_2+...+\kappa_{\nu}x_{\nu}}{\kappa_1+\kappa_2+...+\kappa_{\nu}})^{\kappa_1+\kappa_2+...+\kappa_{\nu}}] \geq \ln(x_1^{\kappa_1}x_2^{\kappa_2}...x_{\nu}^{\kappa_{\nu}})$ $\Leftrightarrow (\kappa_1+\kappa_2+...+\kappa_{\nu})\cdot \ln(\dfrac{\kappa_1x_1+\kappa_2x_2+...+\kappa_{\nu}x_{\nu}}{\kappa_1+\kappa_2+...+\kappa_{\nu}})\geq$ $\kappa_1\cdot \ln(x_1)+\kappa_2\cdot \ln(x_2)+...+\kappa_{\nu}\cdot \ln(x_{\nu})$

Αυτή όμως προκύπτει από την σταθμισμένη ανισότητα Jensen

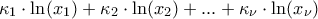
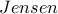για την κοίλη συνάρτηση ln(x)

.

#7

ΗρακληςΕυαγγελινος έγραψε: 4) Αν $\alpha, \beta, \gamma \in R^{+}$ να αποδειχθεί ότι: $\frac{1}{(\alpha+\beta)\beta}+\frac{1}{(\beta+\gamma)\gamma}+\frac{1}{(\gamma+\alpha)\alpha} \geq \frac{9}{2(\alpha\beta+\beta\gamma+\gamma\alpha)}$

Από ΑΜ-ΓΜ είναι

$\displaystyle{\frac{1}{(a+b)b}+\frac{1}{(b+c)c}+\frac{1}{(c+a)a}\geq \frac{3}{\sqrt[3]{abc(a+b)(b+c)(c+a)}}}$

οπότε αρκεί

$\displaystyle{2(ab+bc+ca)\geq 3\sqrt[3]{abc(a+b)(b+c)(c+a)}}$

το οποίο είναι άμεσο πάλι από την ΑΜ-ΓΜ στους τρεις αριθμούς $\displaystyle{ab+ac,bc+ba,ca+cb.}$

ΗρακληςΕυαγγελινος · #8

1) Απόδειξη
Γνωρίζουμε ότι:
$\mid \alpha + \beta \mid \leq \mid \alpha \mid + \mid \beta \mid, \mid \beta + \gamma \mid \leq \mid \beta \mid + \mid \gamma \mid, \mid \gamma + \alpha \mid \leq \mid \gamma \mid + \mid \alpha \mid \Rightarrow$
$\frac{1}{\mid \alpha + \beta \mid} \geq \frac{1}{\mid \alpha \mid + \mid \beta \mid}, \frac{1}{\mid \beta + \gamma \mid} \geq \frac{1}{\mid \beta \mid + \mid \gamma \mid}, \frac{1}{\mid \gamma + \alpha \mid} \geq \frac{1}{\mid \gamma \mid + \mid \alpha \mid} \Rightarrow$
(1) $\frac{1}{\mid \alpha + \beta \mid}+\frac{1}{\mid \beta + \gamma \mid} + \frac{1}{\mid \gamma + \alpha \mid} \geq \frac{1}{\mid \alpha \mid + \mid \beta \mid} + \frac{1}{\mid \beta \mid + \mid \gamma \mid} + \frac{1}{\mid \gamma \mid + \mid \alpha \mid}$

Εφαρμόζω την 1η Ανισότητα Cauchy για τους $\frac{1}{\mid \alpha \mid + \mid \beta \mid}, \frac{1}{\mid \beta \mid + \mid \gamma \mid}, \frac{1}{\mid \gamma \mid + \mid \alpha \mid}$ και έχω:

$\frac{\frac{1}{\mid \alpha \mid + \mid \beta \mid} + \frac{1}{\mid \beta \mid + \mid \gamma \mid} + \frac{1}{\mid \gamma \mid + \mid \alpha \mid}}{3} \geq \sqrt[3]{\frac{1}{\mid \alpha \mid + \mid \beta \mid} \cdot \frac{1}{\mid \beta \mid + \mid \gamma \mid} \cdot \frac{1}{\mid \gamma \mid + \mid \alpha \mid}}$
$\stackrel{(2)}{\Leftrightarrow} \frac{1}{\mid \alpha \mid + \mid \beta \mid} + \frac{1}{\mid \beta \mid + \mid \gamma \mid} + \frac{1}{\mid \gamma \mid + \mid \alpha \mid} \geq \frac{3}{\sqrt[3]{(\mid \alpha \mid + \mid \beta \mid) \cdot (\mid \beta \mid + \mid \gamma \mid) \cdot (\mid \gamma \mid + \mid \alpha \mid)}}$

Εφαρμόζω την ανισότητα Cauchy για τους αριθμούς $(\mid \alpha \mid + \mid \beta \mid) , (\mid \beta \mid + \mid \gamma \mid) , (\mid \gamma \mid + \mid \alpha \mid)$ και έχω:

$\frac{(\mid \alpha \mid + \mid \beta \mid) + (\mid \beta \mid + \mid \gamma \mid) + (\mid \gamma \mid + \mid \alpha \mid)}{3} \geq \sqrt[3]{(\mid \alpha \mid + \mid \beta \mid) \cdot (\mid \beta \mid + \mid \gamma \mid) \cdot (\mid \gamma \mid + \mid \alpha \mid)}$

$\Leftrightarrow \frac{2(\mid \alpha \mid + \mid \beta \mid + \mid \gamma \mid)}{3} \geq \sqrt[3]{(\mid \alpha \mid + \mid \beta \mid) \cdot (\mid \beta \mid + \mid \gamma \mid) \cdot (\mid \gamma \mid + \mid \alpha \mid)} (3)$

Αντιστρέφω την ανισότητα (3) και πολλαπλασιάζω τα μέλη της με 3. Τότε έχω:

$\frac{3}{\sqrt[3]{(\mid \alpha \mid + \mid \beta \mid) \cdot (\mid \beta \mid + \mid \gamma \mid) \cdot (\mid \gamma \mid + \mid \alpha \mid)}} \geq \frac{9}{2}\frac{1}{\mid \alpha \mid + \mid \beta \mid + \mid \gamma \mid} (4)$

Από τις (1), (2), (3), (4) έχω:

$\frac{1}{\mid \alpha + \beta \mid}+ \frac{1}{\mid \beta + \gamma \mid}+ \frac{1}{\mid \gamma + \alpha \mid} \geq \frac{1}{\mid \alpha \mid + \mid \beta \mid} + \frac{1}{\mid \beta \mid + \mid \gamma \mid} + \frac{1}{\mid \gamma \mid + \mid \alpha \mid} \geq \frac{3}{\sqrt[3]{(\mid \alpha \mid + \mid \beta \mid) \cdot (\mid \beta \mid + \mid \gamma \mid) \cdot (\mid \gamma \mid + \mid \alpha \mid)}}$ \displaystyle{\geq \frac{9}{2}\frac{1}{\mid \alpha \mid + \mid \beta \mid + \mid \gamma \mid} ,

Δηλαδή απεδείχθει η άσκηση

\frac{1}{\mid \alpha + \beta \mid} + \frac{1}{\mid \beta + \gamma \mid} + \frac{1}{\mid \gamma + \alpha \mid} \geq \frac{9}{2}\frac{1}{\mid \alpha \mid + \mid \beta \mid + \mid \gamma \mid} 2) <span style="text-decoration:underline">Απόδειξη</span>

Από την ανισότητα Cauchy:

\frac{x_1+x_2+...+x_{\nu}}{\nu} \geq \sqrt[\nu]{x_1x_2...x_{\nu}} \Rightarrow

\frac{\overbrace{x_1+x_1+...+x_1}^{\kappa_1 }+\overbrace{x_2+x_2+...+x_2}^{\kappa_2}+...+\overbrace{x_\nu+x_\nu+...+x_\nu}^{\kappa_{\nu}}}{\kappa_1+\kappa_2+...+\kappa_{\nu}}} $\geq \sqrt[\kappa_1+\kappa_2+...+\kappa_{\nu}]{(\underbrace{x_1x_1...x_1}_{\kappa_1})(\underbrace{x_2x_2...x_2}_{\kappa_2})...(\underbrace{x_\nu x_\nu ...x_\nu}_{\kappa_{\nu}})}$

$\Leftrightarrow \frac{\kappa_1x_1+\kappa_2x_2+...+\kappa_{\nu}x_\nu}{\kappa_1+\kappa_2+...+\kappa_{\nu}}\geq \sqrt[\kappa_1+\kappa_2+...+\kappa_{\nu}]{x_1^{\kappa_1}x_2^{\kappa_2}...x_\nu^{\kappa_{\nu}}}$ $\Leftrightarrow(\frac{\kappa_1x_1+\kappa_2x_2+...+\kappa_{\nu}x_{\nu}}{\kappa_1+\kappa_2+...+\kappa_{\nu}})^{\kappa_1+\kappa_2+\kappa_{\nu}} \geq x_1^{\kappa_{1}}x_2^{\kappa_2}...x_{\nu}^{\kappa_{\nu}}$

3) Απόδειξη

Από ανισότητα Cauchy έχω:

$\frac{1+2+...+3\nu}{3\nu}>\sqrt[3\nu]{1 \cdot 2 \cdot \cdot \cdot 3\nu} \Leftrightarrow$

$\frac{(1+3\nu)\cdot 3\nu}{2\cdot 3\nu} = \frac{1+3\nu}{2}>\sqrt[3\nu]{1 \cdot 2 \cdot \cdot \cdot 3\nu} \Leftrightarrow \frac{(1+3\nu)^3}{8}>\sqrt[\nu]{1 \cdot 2 \cdot \cdot \cdot 3\nu} \Leftrightarrow$ $(1+3\nu)^2(\frac{1+3\nu}{8})>\sqrt[\nu]{1 \cdot 2 \cdot \cdot \cdot 3\nu}$ ,

αλλά
$3\nu > \frac{1+3\nu}{8}$ , άρα κατά μείζονα λόγον $3\nu(1+3\nu)^2>\sqrt[\nu]{1 \cdot 2 \cdot \cdot \cdot 3\nu}$

4) Απόδειξη

Εφαρμόζω την 1η ανισότητα Cauchy για τους
$\frac{1}{(\alpha+\beta)\beta} , \frac{1}{(\beta+\gamma)\gamma} , \frac{1}{(\gamma+\alpha)\alpha} \quad$

και στη συνέχεια τη 2η ανισότητα για τους
$\frac{1}{(\alpha+\beta)\gamma} , \frac{1}{(\beta+\gamma)\alpha} , \frac{1}{(\gamma+\alpha)\beta}$

και έχω:

$\frac{1}{(\alpha+\beta)\beta}+\frac{1}{(\beta+\gamma)\gamma}+\frac{1}{(\gamma+\alpha)\alpha} \geq 3\sqrt[3]{\frac{1}{(\alpha+\beta)\beta(\beta+\gamma)\gamma(\gamma+\alpha)\alpha}} = 3\sqrt[3]{\frac{1}{(\alpha+\beta)\gamma}\frac{1}{(\beta+\gamma)\alpha}\frac{1}{(\gamma+\alpha)\beta}}$ $\geq 3\frac{3}{(\alpha+\beta)\gamma+(\beta+\gamma)\alpha+(\gamma+\alpha)\beta} = \frac{9}{2(\alpha\beta+\beta\gamma+\alpha\gamma)}$

Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Re: Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Re: Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Re: Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Re: Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Re: Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Re: Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Re: Ασκήσεις στην Ανισότητα Cauchy - B' Ομάδα

Μέλη σε σύνδεση