 (Sakis) κινείται με σταθερή ταχύτητα
(Sakis) κινείται με σταθερή ταχύτητα  , από το άκρο
, από το άκρο  της διαμέτρου
της διαμέτρου ενός ημικυκλίου , προς το άλλο άκρο
 . Ένα εκπαιδευμένο έντομο
. Ένα εκπαιδευμένο έντομο  (S'knipa)
(S'knipa)κινείται επί του τόξου παραμένοντας πάντα στην ίδια κατακόρυφο με τον εκπαιδευτή της .
α) Βρείτε τη μέση ταχύτητα του εντόμου ( μόριο
 )
)β) Είναι σταθερή η ταχύτητα του εντόμου ? ( μόρια
 )
)γ) Ποιά είναι η μεγαλύτερη ταχύτητα του εντόμου ( πολλά μόρια )
δ) Όταν ο εκπαιδευτής θα έχει διανύσει το
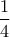 της διαδρομής , τι κλάσμα της δικής της
της διαδρομής , τι κλάσμα της δικής τηςδιαδρομής θα έχει διανύσει η σκνίπα ? ( μόρια
 )
)ε) Ποια είναι η ταχύτητα του ζωυφίου , όταν αυτό βρεθεί στην κορυφή ? (
 -(πολλά) μόρια ) .
-(πολλά) μόρια ) .στ) Η ταχύτητα του
 πλησιάζοντας στο
πλησιάζοντας στο  αυξάνει , μειώνεται ή παραμένει
αυξάνει , μειώνεται ή παραμένεισταθερή ? ( δυστυχώς μόρια τέλος - συμπληρώθηκαν τα
 στην προηγούμενη απάντηση ! )
στην προηγούμενη απάντηση ! )
 , τόσο θα χρειασθεί και η S'knipa, οπότε
, τόσο θα χρειασθεί και η S'knipa, οπότε 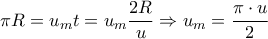
 μεταβάλλεται.
μεταβάλλεται.
 (αφού η κατακόρυφη συνιστώσα της ταχύτητας του
(αφού η κατακόρυφη συνιστώσα της ταχύτητας του  ( σκνίπα) και
( σκνίπα) και  .
. και άρα
και άρα  . Η σταθερή γραμμική ταχύτητα είναι
. Η σταθερή γραμμική ταχύτητα είναι  ενώ από την
ενώ από την  έχουμε :
έχουμε :  . Με προφανώς
. Με προφανώς  την ταχύτητα της σκνίπας.
την ταχύτητα της σκνίπας. θα είναι
θα είναι 
 θα έχουμε
θα έχουμε 
 επειδή η συνάρτηση
επειδή η συνάρτηση  είναι γνήσια φθίνουσα η συνάρτηση
είναι γνήσια φθίνουσα η συνάρτηση  είναι γνήσια αύξουσα .
είναι γνήσια αύξουσα .