Σελίδα 1 από 1
πολυωνυμοεκθετική
Δημοσιεύτηκε: Δευ Μαρ 20, 2017 7:55 pm
από KARKAR
Να λυθεί η εξίσωση :

( Ακατάλληλη για διαγώνισμα ! )
Re: πολυωνυμοεκθετική
Δημοσιεύτηκε: Τρί Μαρ 21, 2017 2:15 pm
από Tolaso J Kos
KARKAR έγραψε:Να λυθεί η εξίσωση :

( Ακατάλληλη για διαγώνισμα ! )
Επαναφέρω το θέμα (το οποίο δε κατάφερα να λύσω ) και δίνω μόνο τις λύσεις

,

. ( τις οποίες βρήκα με λογισμικό )
Re: πολυωνυμοεκθετική
Δημοσιεύτηκε: Τρί Μαρ 21, 2017 3:09 pm
από matha
Η συνάρτηση

έχει

αφού

Άρα η

δεν έχει περισσότερες από δύο ρίζες.
Re: πολυωνυμοεκθετική
Δημοσιεύτηκε: Τρί Μαρ 21, 2017 3:33 pm
από Σταμ. Γλάρος
KARKAR έγραψε:Να λυθεί η εξίσωση :

( Ακατάλληλη για διαγώνισμα ! )
Καλησπέρα. Μια προσπάθεια εκτός φακέλου με ύλη Γ΄Λυκείου.
Θεωρώ την συνάρτηση

.
Είναι παραγωγίσιμη ως πράξεις παραγωγίσιμων συναρτήσεων με

Ομοίως

παραγωγίσιμη ως πράξεις παραγωγίσιμων συναρτήσεων με
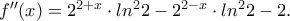
Επίσης
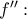
παραγωγίσιμη ως πράξεις παραγωγίσιμων συναρτήσεων με

Στη συνέχεια έχουμε:

Τώρα ισχύει :

γνησίως φθίνουσα στο

και
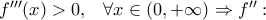
γνησίως αύξουσα στο

.
Συνεπώς η

παρουσιάζει ολικό ελάχιστο στο

το

Είναι :

το οποίο ισχύει.
Άρα

.
Προφανείς λύσεις της

είναι οι

και

Έστω ότι η

έχει τρεις λύσεις :

στο

με

.
Ισχύουν οι προϋποθέσεις του Θ. Rolle για την

στα διαστήματα :
![[p_{1}, p_{2}] [p_{1}, p_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/e2297b67765bb9b601ad1ecde550b6da.png)
και
![[p_{2}, p_{3}] [p_{2}, p_{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/841d39d7ad63927fef61231822c00f6b.png)
.
Επομένως υπάρχουν

και

τέτοια ώστε:
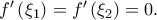
Επίσης ισχύουν οι προϋποθέσεις του Θ. Rolle για την

στο διαστημα :
![[\xi_{1}, \xi_{2}] [\xi_{1}, \xi_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/497f7459a7c46d0e77f070649f3cd7d8.png)
.
Επομένως υπάρχει

τέτοιο ώστε:

Άτοπο.
Άρα μοναδικές λύσεις οι

και

Φιλικά
Σταμ. Γλάρος
ΥΓ. Τώρα βλέπω ότι στην ουσία λέμε τα ίδια με τον matha . Την αφήνω για τον κόπο της πληκτρολόγησης.
Re: πολυωνυμοεκθετική
Δημοσιεύτηκε: Τρί Μαρ 21, 2017 3:57 pm
από Τσιαλας Νικολαος
Χωρίς παρεξήγηση, μπορούμε να σταματήσουμε στην δεύτερη παράγωγο χρησημοποιώντας την γνωστή σχολική ανισότητα χ + 1/χ >2 (ή ίσο) η' όπως το πήγε ο matha. Πάντως δεν είναι ιδιαίτερα δύσκολη για διαγώνισμα!!

Re: πολυωνυμοεκθετική
Δημοσιεύτηκε: Τρί Μαρ 21, 2017 9:05 pm
από KARKAR
Διαιρώντας δια

, η εξίσωση γίνεται :

και έτσι έχουμε
την "εντελώς προφανή " ρίζα

και τη "σχεδόν προφανή"

,
επιπλέον δε κάνουμε ευκολότερα τις πράξεις

Για αποζημίωση βάζω το σχήμα της άσκησης .

- sxima.png (14.16 KiB) Προβλήθηκε 409 φορές
Η συνάρτηση

θα μπορούσε να αποκληθεί "ψευδοπαραβολή" .
Δύο "γνήσιες" παραβολές , πόσα το πολύ κοινά σημεία μπορούν να έχουν ;
 ( Ακατάλληλη για διαγώνισμα ! )
( Ακατάλληλη για διαγώνισμα ! ) ( Ακατάλληλη για διαγώνισμα ! )
( Ακατάλληλη για διαγώνισμα ! ) ( Ακατάλληλη για διαγώνισμα ! )
( Ακατάλληλη για διαγώνισμα ! )( Ακατάλληλη για διαγώνισμα ! )
 ,
,  . ( τις οποίες βρήκα με λογισμικό )
. ( τις οποίες βρήκα με λογισμικό ) έχει
έχει

 δεν έχει περισσότερες από δύο ρίζες.
δεν έχει περισσότερες από δύο ρίζες.( Ακατάλληλη για διαγώνισμα ! )
 .
. 
 παραγωγίσιμη ως πράξεις παραγωγίσιμων συναρτήσεων με
παραγωγίσιμη ως πράξεις παραγωγίσιμων συναρτήσεων με 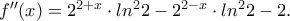
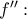 παραγωγίσιμη ως πράξεις παραγωγίσιμων συναρτήσεων με
παραγωγίσιμη ως πράξεις παραγωγίσιμων συναρτήσεων με 

 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο 
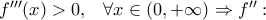 γνησίως αύξουσα στο
γνησίως αύξουσα στο  .
. παρουσιάζει ολικό ελάχιστο στο
παρουσιάζει ολικό ελάχιστο στο  το
το 
 το οποίο ισχύει.
το οποίο ισχύει. .
. είναι οι
είναι οι  και
και 
 έχει τρεις λύσεις :
έχει τρεις λύσεις :  στο
στο  με
με  .
. στα διαστήματα :
στα διαστήματα : ![[p_{1}, p_{2}] [p_{1}, p_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/e2297b67765bb9b601ad1ecde550b6da.png) και
και ![[p_{2}, p_{3}] [p_{2}, p_{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/841d39d7ad63927fef61231822c00f6b.png) .
. και
και  τέτοια ώστε:
τέτοια ώστε: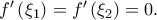
 στο διαστημα :
στο διαστημα : ![[\xi_{1}, \xi_{2}] [\xi_{1}, \xi_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/497f7459a7c46d0e77f070649f3cd7d8.png) .
. τέτοιο ώστε:
τέτοιο ώστε:  Άτοπο.
Άτοπο. και
και 
 , η εξίσωση γίνεται :
, η εξίσωση γίνεται :  και έτσι έχουμε
και έτσι έχουμε και τη "σχεδόν προφανή"
και τη "σχεδόν προφανή"  ,
, θα μπορούσε να αποκληθεί "ψευδοπαραβολή" .
θα μπορούσε να αποκληθεί "ψευδοπαραβολή" .