Καλησπέρα.
Κατά αρχάς να ευχαριστήσω τον κ. Λάμπρου διότι με έναν πολύ απλό τρόπο και συγχρόνως άψογο μαθηματικά,
έδειξε ότι κάπου υπάρχει αρνητική τιμή της

.
Ούτε που πέρασε από το μυαλό αν και το συστήνουμε στους μαθητές...

Επανέρχομαι μετά από καιρό στο δεύτερο υποερώτημα του ενδιαφέροντος θέματος.
Η συνάρτησή μας για

, παίρνει την μορφή

.
Πρώτα απ΄ όλα με το Geogebra προσπάθησα να κάνω την γραφική παράσταση της συνάρτησης .
Σε πρώτη φάση το αποτέλεμα ήταν το παρακάτω:

- Κοινά σημεία 1.png (7.59 KiB) Προβλήθηκε 2265 φορές
Όπως φαίνεται στο παραπάνω σχήμα η

έχει, εμφανώς, δύο σημεία τομής με τον
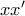
.
Όμως παρατηρείται το εξής φαινόμενο. Το Geogebra προσδιορίζει μόνο το ένα σημείο τομής, το

.
Όσες φορές και εάν προσπάθησα δεν μπόρεσα να προσδιορίσω το άλλο σημείο.
Το Geogebra ... πεισματικά αγνοούσε το άλλο. Ή πατούσε ξανά και ξανά πάνω στο

ή σπανιότερα έβγαζε αδύνατο.
Αγνόησα λοιπόν το Geogebra και άρχισα να ασχολούμαι με το Θεώρημα Bolzano.
Με το κομπουτεράκι βρήκα

και

.
Έτσι, λοιπόν, βρήκα ότι το άλλο σημείο τομής έχει τετμημένη

.
Όμως παρέμενε η απορία. Τι έπαθε το Geogebra ;
Έτσι, λοιπόν, έδωσα την συνάρτηση στον γιο μου Βασίλη, ο οποίος είναι τελοιόφοιτος του ΕΜΠ στο τμήμα Μηχανολόγων.
Αυτός ισχυρίζεται ότι μπορεί να βρει την λύση μιας μη γραμμικής εξίσωσης .... εύκολα!
Φανταστείτε την έκπληξή του! Αν και η γραφική παράσταση της συνάρτησησης δείχνει καθαρά 2 σημεία τομής με τον
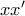
,
έβρισκε μόνο την λύση

.
Αρχίσαμε, λοιπόν, να ψάχνουμε μαζί. Χρησιμοποίησε το βιβλίο: " Αριθμητική Ανάλυση για Μηχανικούς" των Κ.Χ.Γιανάκογλου,
Ι. Αναγνωστόπουλου και Γ. Μπεργελέ , Εκδόσεις ΕΜΠ του τμήματος Μηχανολόγων Μηχανικών.
Αυτός υπολόγιζε την ρίζα με την επαναληπτική μέδοδο Newton -Raphson. Στην σελίδα 2.14 διαβάζουμε:
Η δημοφιλέστερη ανοιχτή μέδοδος (για τον υπολογισμό ρίζας μη γραμμικής συνάρτησης) είναι η Newton-Raphson (N-R) ,
το βασικότερο πλεονέκτημα της οποίας είναι ότι επιτυγχάνει τετραγωνική σύγκλιση κοντά στη ρίζα.
Αμέσως ξύπνησαν ... οι αναμνήσεις. Αριθμητική ανάλυση, Μέθοδος Διχοτόμησης , Μέθοδος Ν-R, κλπ...
Η μέθοδος N-R, δημιουργεί έναν αναδρομικό τύπο ο οποίος προκύπτει από σειρά Taylor η οποία συγκλίνει στην ρίζα.
Στην ίδια σελίδα του παραπάνω βιβλίου έχουμε και την γεωμετρική ερμηνεία της μεθόδου:
Η εφαπτομένη (παράγωγος) της συνάρτησης  σε ένα σημείο
σε ένα σημείο  τέμνει τον άξονα
τέμνει τον άξονα 
σε σημείο  το οποίο προσεγγίζει περισσότερο τη ρίζα .
το οποίο προσεγγίζει περισσότερο τη ρίζα .
Εννοείται ότι πρέπει η συνάρτηση να είναι παραγωγίσιμη.
Και στην παρακάτω σελίδα 2.17 νομίζω ότι βρίσκεται η ... λύση του μυστηρίου!
... η μέθοδος Ν-R είναι ευαίσθητη στην επιλογή της τιμής εκκίνησης και υπάρχει περίπτωση να μην συγκλίνει
εάν αυτή δεν βρίσκεται αρκετά "κοντά" στη ρίζα της εξίσωσης.
Αυτό είναι !
Ακόμα και αν θεωρήσουμε ως αρχική τιμή εκκίνησης της μεθόδου

με όριο σύκλισης

προέκυπτε λύση

!
Εξ' άλλου το βιβλίο αναφέρει πάλι στην σελίδα 2.17 :
Σε δύσκολες περιπτώσεις μπορεί να συνδυάζεται με την μέθοδο της διχοτόμησης, ώστε να εντοπίζεται πρώτα η περιοχή της ρίζας .
Πράγματι! Έπρεπε από την αρχή να αξιοποιήσουμε το Θ. Bolzano!!!
Με αρχική τιμή εκκίνησης της μεθόδου

με όριο σύκλισης

,
μετα από
3 μόλις επαναλήψεις έχουμε σύγλιση στο

.
Τα παραπάνω φαίνονται στο εξής σχήμα:

- Κοινά Σημεία 2 .png (164.41 KiB) Προβλήθηκε 2265 φορές
Στο σχήμα παρατηρούμε τα εξής :
1ο Βήμα : Η εφαπτομένη της

στο

τέμνει τον άξονα
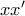
στο σημείο

.
2ο Βήμα : H κάθετη στον
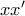
στο σημείο

τέμνει την

στο

.
Η εφαπτομένη της

στο

τέμνει τον άξονα
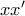
στο σημείο

.
3ο Βήμα : H κάθετη στον
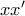
στο σημείο

τέμνει την

στο

.
Η εφαπτομένη της

στο

τέμνει τον άξονα
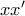
στο σημείο

.
Βλέπουμε πώς συγκλίνει το
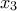
στην ρίζα

με αρχική τιμή

.
Επίσης η "κόκκινη ευθεία " ευθεία είναι η εφαπτομένη της

στο

.
Παρατηρήστε ότι "ταυτίζονται" η εφαπτομένη και η γραφική παράσταση !
Αν μπορούσαμε να φτιάξουμε και ασύμπτωτη σίγουρα και αυτή θα ταυτιζόταν με τις παραπάνω ...
Αυτός, νομίζω, είναι και ο λόγος για τον οποίο το πρόγραμμα αδυνατεί να δώσει λύση.
Συγγνώμη εάν κούρασα...
Θα περιμένω σχόλια από τους πολύ σπουδαιότερους από εμένα στο

.
Φιλικά
Σταμ. Γλάρος
 και
και  , έχουν δύο ακριβώς κοινά σημεία .
, έχουν δύο ακριβώς κοινά σημεία .  , βρείτε προσεγγιστικά ( ή με ακρίβεια ! ) τις τετμημένες
, βρείτε προσεγγιστικά ( ή με ακρίβεια ! ) τις τετμημένες  και
και  , έχουν δύο ακριβώς κοινά σημεία .
, έχουν δύο ακριβώς κοινά σημεία .  , βρείτε προσεγγιστικά ( ή με ακρίβεια ! ) τις τετμημένες
, βρείτε προσεγγιστικά ( ή με ακρίβεια ! ) τις τετμημένες και
, έχουν δύο ακριβώς κοινά σημεία .
, βρείτε προσεγγιστικά ( ή με ακρίβεια ! ) τις τετμημένες
 .
. Άρα κοινό σημείο των
Άρα κοινό σημείο των  είναι το
είναι το 

 .
.

 .
.

 .
. .
. στο
στο ![\left [ k+e^{-e^{k+1}} , k+\frac{1}{2} \right ] \left [ k+e^{-e^{k+1}} , k+\frac{1}{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/8eff418697c985f95aaedd97ee5775bc.png) .
. της
της  στο
στο  .
. είναι και το
είναι και το 
 έχουν τρία σημεία τομής με τετμημένες
έχουν τρία σημεία τομής με τετμημένες  , με
, με  .
. είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  καθώς και η
καθώς και η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  .
. είναι γνησίως αύξουσα , άρα και 1-1.
είναι γνησίως αύξουσα , άρα και 1-1. στα
στα ![[x_{1} , x_{2} ] [x_{1} , x_{2} ]](/forum/ext/geomar/texintegr/latexrender/pictures/0aff5bd80609d3d68d0e3692e352834e.png) ,
, ![[x_{2} , x_{3} ] [x_{2} , x_{3} ]](/forum/ext/geomar/texintegr/latexrender/pictures/0b228b7cf12011a9192cfaf9ca9d0142.png)
 . ΑΤΟΠΟ αφού η
. ΑΤΟΠΟ αφού η  είναι 1-1.
είναι 1-1. έχουν δύο ακριβώς κοινά σημεία .
έχουν δύο ακριβώς κοινά σημεία . .
στο
.
 έχει κάπου αρνητική τιμή: Αφού ο λογάριθμος στο
έχει κάπου αρνητική τιμή: Αφού ο λογάριθμος στο  τείνει στο
τείνει στο  καθώς
καθώς  ενώ όλοι οι άλλοι όροι έχουν (πεπερασμένο) όριο, σημαίνει ότι κοντά και δεξιά του
ενώ όλοι οι άλλοι όροι έχουν (πεπερασμένο) όριο, σημαίνει ότι κοντά και δεξιά του  είναι
είναι  . Και λοιπά.
. Και λοιπά. .
. , παίρνει την μορφή
, παίρνει την μορφή  .
.  έχει, εμφανώς, δύο σημεία τομής με τον
έχει, εμφανώς, δύο σημεία τομής με τον 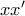 .
.  .
.
 και
και  .
. .
.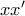 ,
, .
. σε ένα σημείο
σε ένα σημείο  τέμνει τον άξονα
τέμνει τον άξονα 
 το οποίο προσεγγίζει περισσότερο τη ρίζα .
το οποίο προσεγγίζει περισσότερο τη ρίζα . με όριο σύκλισης
με όριο σύκλισης 
 !
! με όριο σύκλισης
με όριο σύκλισης  ,
,  .
. στο
στο  τέμνει τον άξονα
τέμνει τον άξονα 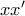 στο σημείο
στο σημείο  .
.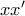 στο σημείο
στο σημείο  τέμνει την
τέμνει την  στο
στο  .
. στο
στο  τέμνει τον άξονα
τέμνει τον άξονα 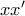 στο σημείο
στο σημείο  .
.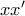 στο σημείο
στο σημείο  τέμνει την
τέμνει την  στο
στο  .
. στο
στο  τέμνει τον άξονα
τέμνει τον άξονα 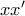 στο σημείο
στο σημείο  .
.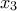 στην ρίζα
στην ρίζα  με αρχική τιμή
με αρχική τιμή  .
. στο
στο  .
.