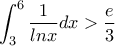 ,
, β)
 , ....γ)
, ....γ) 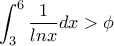 , ...δ)
, ...δ) 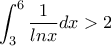
Συντονιστής: Γιώργος Ρίζος
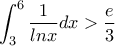 ,
,  , ....γ)
, ....γ) 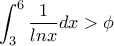 , ...δ)
, ...δ) 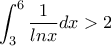
α), β), γ) Η δεύτερη και η τρίτη είναι αφύσικες αφού τοKARKAR έγραψε:Δείξτε , αυστηρά με τη σειρά της εκφώνησης , ότι : α),
β), ....γ)
, ...δ)
 και το
και το  δεν μπαίνουν στους συλλογισμούς. Δεδομένου ότι η
δεν μπαίνουν στους συλλογισμούς. Δεδομένου ότι η 
 για
για  έχουμε την εξής ανισότητα που πιστεύω ότι δεν είναι όσο γνωστή θα έπρεπε: Για
έχουμε την εξής ανισότητα που πιστεύω ότι δεν είναι όσο γνωστή θα έπρεπε: Για  έχουμε
έχουμε 

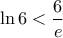 που δίνει είναι μεγάλη για την άσκηση, αλλά μπορούμε εύκολα να την βελτιώσουμε:
που δίνει είναι μεγάλη για την άσκηση, αλλά μπορούμε εύκολα να την βελτιώσουμε: 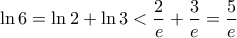
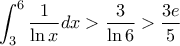

Να λοιπόν που μάθαμε και μια καινούρια ανισότηταMihalis_Lambrou έγραψε:

 , ισχύουν :
, ισχύουν : , ...β)
, ...β)  , ....γ)
, ....γ)  . Αντιστρέφοντας και βρίσκοντας
. Αντιστρέφοντας και βρίσκοντας Άκομψος τρόπος: Δεδομένου ότι η πραγματική τιμή του ολοκληρώματος, σύμφωνα με λογισμικό, είναιKARKAR έγραψε:δ)
 , σημαίνει ότι η ανισότητα είναι πολύ σφικτή. Άρα οι εκτιμήσεις πρέπει να είναι "με ελάχιστο περίσσευμα".
, σημαίνει ότι η ανισότητα είναι πολύ σφικτή. Άρα οι εκτιμήσεις πρέπει να είναι "με ελάχιστο περίσσευμα". το δοθέν ισούται με
το δοθέν ισούται με ![\displaystyle \int_{\ln 3}^{\ln 6}\frac{e^y}{y}dy \ge \int_{\ln 3}^{\ln 6}\frac{1+y+y^2/2 +y^3/6}{y}dy = \left [ \ln y + y+ y^2/6 + y^3/24 \right ]_{\ln 3} ^{\ln 6} \displaystyle \int_{\ln 3}^{\ln 6}\frac{e^y}{y}dy \ge \int_{\ln 3}^{\ln 6}\frac{1+y+y^2/2 +y^3/6}{y}dy = \left [ \ln y + y+ y^2/6 + y^3/24 \right ]_{\ln 3} ^{\ln 6}](/forum/ext/geomar/texintegr/latexrender/pictures/cd193ee3d48dac0c4a442e7b1cd4538a.png)
 ), βρίσκουμε ότι το ολοκήρωμα είναι όντως
), βρίσκουμε ότι το ολοκήρωμα είναι όντως  (το ... μισοέκανα).
(το ... μισοέκανα).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες