Demetres έγραψε: ↑Σάβ Οκτ 28, 2017 12:21 pm
Η απάντηση είναι 4! Εκπληκτικό ε; Δοκιμάστε το ξανά!
Το μυστικό είναι στην λέξη αναποδογύρισμα. Αυτό είναι διαφορετικό από την ανάκλαση.
Πράγματι, εκπληκτικό! Το πιο εκπληκτικό είναι ότι για οποιοδήποτε μέγεθος κομματιού από
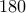
έως
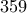
μοίρες χρειάζονται

προσπάθειες... (αν δεν κάνω λάθος)!
Στη δικιά μου λύση πράγματι δεν σκεφτόμουν ότι με το αναποδογύρισμα άλλαζαν τα αριστερά με τα δεξιά...

Η λογική με την οποία μου βγήκε το λανθασμένο αποτέλεσμα
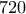
ήταν η εξής:
Αφού το γλασαρισμένο τμήμα του κέικ θα αναποδογύριζε με τη σειρά (εδώ ήταν το λάθος!), βρήκα το ΕΚΠ των

και

, που είναι το

.
Τόσες μοίρες θα είχαμε διανύσει κόβοντας μέχρι να ξαναφτάσουμε στην αρχή. Άρα το γλάσο θα ήταν πάλι όλο στην ίδια πλευρά. Θα είχαμε διανύσει

κύκλους κόβοντας, που επειδή είναι περιττός αριθμός, σημαίνει ότι το γλάσο θα ήταν όλο στην κάτω πλευρά, κάνοντας

κοψιές. Άρα με ακόμα

κοψιές θα ξαναγύριζε το γλάσο όλο στην πάνω πλευρά!
Όταν ήρθε η αρνητική απάντηση για το αποτέλεσμα, έφτιαξα ένα προγραμματάκι σε C που εξομοίωνε την όλη διαδικασία (με το ίδιο λανθασμένο σκεπτικό) και μου έβγαζε το ίδιο λανθασμένο αποτέλεσμα με εμένα!
Πλέον (θέλω να πιστεύω ότι) διόρθωσα το προγραμματάκι. Δίνει για όλα τα πιθανά μεγέθη κομματιών από

έως

μοίρες των αριθμό των βημάτων για να ξαναπάρουμε το κέικ όπως ήταν στην αρχή:
f-1 : 720
f-2 : 360
f-3 : 240
f-4 : 180
f-5 : 144
f-6 : 120
f-7 : 5304
f-8 : 90
f-9 : 80
f-10 : 72
f-11 : 2112
f-12 : 60
f-13 : 1512
f-14 : 1300
f-15 : 48
f-16 : 1012
f-17 : 924
f-18 : 40
f-19 : 684
f-20 : 36
f-21 : 612
f-22 : 544
f-23 : 480
f-24 : 30
f-25 : 420
f-26 : 364
f-27 : 364
f-28 : 312
f-29 : 312
f-30 : 24
f-31 : 264
f-32 : 264
f-33 : 220
f-34 : 220
f-35 : 220
f-36 : 20
f-37 : 180
f-38 : 180
f-39 : 180
f-40 : 18
f-41 : 144
f-42 : 144
f-43 : 144
f-44 : 144
f-45 : 16
f-46 : 112
f-47 : 112
f-48 : 112
f-49 : 112
f-50 : 112
f-51 : 112
f-52 : 84
f-53 : 84
f-54 : 84
f-55 : 84
f-56 : 84
f-57 : 84
f-58 : 84
f-59 : 84
f-60 : 12
f-61 : 60
f-62 : 60
f-63 : 60
f-64 : 60
f-65 : 60
f-66 : 60
f-67 : 60
f-68 : 60
f-69 : 60
f-70 : 60
f-71 : 60
f-72 : 10
f-73 : 40
f-74 : 40
f-75 : 40
f-76 : 40
f-77 : 40
f-78 : 40
f-79 : 40
f-80 : 40
f-81 : 40
f-82 : 40
f-83 : 40
f-84 : 40
f-85 : 40
f-86 : 40
f-87 : 40
f-88 : 40
f-89 : 40
f-90 : 8
f-91 : 24
f-92 : 24
f-93 : 24
f-94 : 24
f-95 : 24
f-96 : 24
f-97 : 24
f-98 : 24
f-99 : 24
f-100 : 24
f-101 : 24
f-102 : 24
f-103 : 24
f-104 : 24
f-105 : 24
f-106 : 24
f-107 : 24
f-108 : 24
f-109 : 24
f-110 : 24
f-111 : 24
f-112 : 24
f-113 : 24
f-114 : 24
f-115 : 24
f-116 : 24
f-117 : 24
f-118 : 24
f-119 : 24
f-120 : 6
f-121 : 12
f-122 : 12
f-123 : 12
f-124 : 12
f-125 : 12
f-126 : 12
f-127 : 12
f-128 : 12
f-129 : 12
f-130 : 12
f-131 : 12
f-132 : 12
f-133 : 12
f-134 : 12
f-135 : 12
f-136 : 12
f-137 : 12
f-138 : 12
f-139 : 12
f-140 : 12
f-141 : 12
f-142 : 12
f-143 : 12
f-144 : 12
f-145 : 12
f-146 : 12
f-147 : 12
f-148 : 12
f-149 : 12
f-150 : 12
f-151 : 12
f-152 : 12
f-153 : 12
f-154 : 12
f-155 : 12
f-156 : 12
f-157 : 12
f-158 : 12
f-159 : 12
f-160 : 12
f-161 : 12
f-162 : 12
f-163 : 12
f-164 : 12
f-165 : 12
f-166 : 12
f-167 : 12
f-168 : 12
f-169 : 12
f-170 : 12
f-171 : 12
f-172 : 12
f-173 : 12
f-174 : 12
f-175 : 12
f-176 : 12
f-177 : 12
f-178 : 12
f-179 : 12
f-180 : 4
f-181 : 4
f-182 : 4
f-183 : 4
f-184 : 4
f-185 : 4
f-186 : 4
f-187 : 4
f-188 : 4
f-189 : 4
f-190 : 4
f-191 : 4
f-192 : 4
f-193 : 4
f-194 : 4
f-195 : 4
f-196 : 4
f-197 : 4
f-198 : 4
f-199 : 4
f-200 : 4
f-201 : 4
f-202 : 4
f-203 : 4
f-204 : 4
f-205 : 4
f-206 : 4
f-207 : 4
f-208 : 4
f-209 : 4
f-210 : 4
f-211 : 4
f-212 : 4
f-213 : 4
f-214 : 4
f-215 : 4
f-216 : 4
f-217 : 4
f-218 : 4
f-219 : 4
f-220 : 4
f-221 : 4
f-222 : 4
f-223 : 4
f-224 : 4
f-225 : 4
f-226 : 4
f-227 : 4
f-228 : 4
f-229 : 4
f-230 : 4
f-231 : 4
f-232 : 4
f-233 : 4
f-234 : 4
f-235 : 4
f-236 : 4
f-237 : 4
f-238 : 4
f-239 : 4
f-240 : 4
f-241 : 4
f-242 : 4
f-243 : 4
f-244 : 4
f-245 : 4
f-246 : 4
f-247 : 4
f-248 : 4
f-249 : 4
f-250 : 4
f-251 : 4
f-252 : 4
f-253 : 4
f-254 : 4
f-255 : 4
f-256 : 4
f-257 : 4
f-258 : 4
f-259 : 4
f-260 : 4
f-261 : 4
f-262 : 4
f-263 : 4
f-264 : 4
f-265 : 4
f-266 : 4
f-267 : 4
f-268 : 4
f-269 : 4
f-270 : 4
f-271 : 4
f-272 : 4
f-273 : 4
f-274 : 4
f-275 : 4
f-276 : 4
f-277 : 4
f-278 : 4
f-279 : 4
f-280 : 4
f-281 : 4
f-282 : 4
f-283 : 4
f-284 : 4
f-285 : 4
f-286 : 4
f-287 : 4
f-288 : 4
f-289 : 4
f-290 : 4
f-291 : 4
f-292 : 4
f-293 : 4
f-294 : 4
f-295 : 4
f-296 : 4
f-297 : 4
f-298 : 4
f-299 : 4
f-300 : 4
f-301 : 4
f-302 : 4
f-303 : 4
f-304 : 4
f-305 : 4
f-306 : 4
f-307 : 4
f-308 : 4
f-309 : 4
f-310 : 4
f-311 : 4
f-312 : 4
f-313 : 4
f-314 : 4
f-315 : 4
f-316 : 4
f-317 : 4
f-318 : 4
f-319 : 4
f-320 : 4
f-321 : 4
f-322 : 4
f-323 : 4
f-324 : 4
f-325 : 4
f-326 : 4
f-327 : 4
f-328 : 4
f-329 : 4
f-330 : 4
f-331 : 4
f-332 : 4
f-333 : 4
f-334 : 4
f-335 : 4
f-336 : 4
f-337 : 4
f-338 : 4
f-339 : 4
f-340 : 4
f-341 : 4
f-342 : 4
f-343 : 4
f-344 : 4
f-345 : 4
f-346 : 4
f-347 : 4
f-348 : 4
f-349 : 4
f-350 : 4
f-351 : 4
f-352 : 4
f-353 : 4
f-354 : 4
f-355 : 4
f-356 : 4
f-357 : 4
f-358 : 4
f-359 : 4
f-360 : 2
Ο κώδικας για όποιον ενδιαφέρεται:
(έχω αφήσει σε σχόλιο και την αρχική εκδοχή)
Υ.Γ. Νομίζω παλιότερα ο κώδικας φαινόταν κανονικά με τις αλλαγές γραμμών. Ίσως φταίει η τελευταία αναβάθμιση!

Κώδικας: Επιλογή όλων
#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
freopen("pita.out", "w", stdout);
int i, t, c, f, ok;
bool pita[360], pitatmp[360];
for (i=0; i<360; i++)
pita[i]=true;
for (f=1; f<=360; f++) {
c=0; t=0;
for (;;){
/* old
for (i=0; i<f; i++) {
pita[(c+i)%360]=!pita[(c+i)%360];
}
old */
/* new */
for (i=0; i<f; i++) {
pitatmp[i]=pita[(c+i)%360];
}
for (i=0; i<f; i++) {
pita[(c+i)%360]= !pitatmp[f-i-1];
}
/* new */
c=(c+f)%360;
t++;
ok=0;
for (i=0; i<360; i++)
ok=ok+ pita[i];
if (ok==360) {
cout << "f-" << f << " : " << t << "\n";
break;
}
}
}
return 0;
}
 μοιρών. Αφαιρούμε το κομμάτι, το αναποδογυρίζουμε, και το τοποθετούμε αναποδογυρισμένο στην αρχική του θέση. Επαναλαμβάνουμε με το αμέσως επόμενο κομμάτι, που εφάπτεται του πρώτου που κόψαμε. Κόβουμε, αφαιρούμε, αναποδογυρίζουμε, επανατοποθετούμε. Συνεχίζουμε να το κάνουμε αυτό κάθε φορά παίρνοντας το επόμενο ωρολογιακά π.χ. κομμάτι.
μοιρών. Αφαιρούμε το κομμάτι, το αναποδογυρίζουμε, και το τοποθετούμε αναποδογυρισμένο στην αρχική του θέση. Επαναλαμβάνουμε με το αμέσως επόμενο κομμάτι, που εφάπτεται του πρώτου που κόψαμε. Κόβουμε, αφαιρούμε, αναποδογυρίζουμε, επανατοποθετούμε. Συνεχίζουμε να το κάνουμε αυτό κάθε φορά παίρνοντας το επόμενο ωρολογιακά π.χ. κομμάτι.  να βρεθεί πόσες φορές πρέπει να κάνουμε την διαδικασία ώστε να ξαναπάρουμε το κέικ με όλο το γλάσο να βρίσκεται στην πάνω μεριά.
να βρεθεί πόσες φορές πρέπει να κάνουμε την διαδικασία ώστε να ξαναπάρουμε το κέικ με όλο το γλάσο να βρίσκεται στην πάνω μεριά.
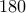 έως
έως 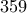 μοίρες χρειάζονται
μοίρες χρειάζονται  προσπάθειες... (αν δεν κάνω λάθος)!
προσπάθειες... (αν δεν κάνω λάθος)! 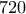 ήταν η εξής:
ήταν η εξής: και
και  , που είναι το
, που είναι το  .
.  κύκλους κόβοντας, που επειδή είναι περιττός αριθμός, σημαίνει ότι το γλάσο θα ήταν όλο στην κάτω πλευρά, κάνοντας
κύκλους κόβοντας, που επειδή είναι περιττός αριθμός, σημαίνει ότι το γλάσο θα ήταν όλο στην κάτω πλευρά, κάνοντας  έως
έως