Σελίδα 1 από 2
Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Πέμ Δεκ 14, 2017 8:12 pm
από KARKAR

- Διαγωνισμός ομορφιάς.png (9.65 KiB) Προβλήθηκε 2025 φορές
Πάνω στη διάμεσο

τριγώνου

, καλούμαστε να εντοπίσουμε σημείο

,
έτσι ώστε :

. Κερδίζει η ομορφότερη λύση . Αλλά τα κριτήρια επιλογής , καθώς
και η σύνθεση της κριτικής επιτροπής δεν προαναγγέλλονται για ευνόητους λόγους .
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Πέμ Δεκ 14, 2017 9:02 pm
από Doloros
(Δεν με ενδιαφέρει η ομορφιά !)

- Διαγωνισμός ομορφιάς.png (36.88 KiB) Προβλήθηκε 2015 φορές
Έστω

το σημείο τομής της

με τον περιγεγραμμένο κύκλο του

.
Η μεσόκάθετος στο
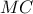
τέμνει στο

την κάθετο επί την

στο σημείο του

.
Ο κύκλος

τέμνει , εν γένει , την

στο

.
Θα επανέλθω μετά από άλλες λύσεις αν έχω κάτι καλύτερο βρει.
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Πέμ Δεκ 14, 2017 9:16 pm
από Γιώργος Ρίζος
Δίχως να θέλω καθόλου να επηρεάσω την αμερόληπτη
κρητική επιτροπή:

- 14-12-2017 Γεωμετρία.jpg (36.29 KiB) Προβλήθηκε 2008 φορές
Από τον πανέμορφο Ν Ημιτόνων στα

έχουμε

και

.
Αφού

, είναι
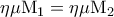
οπότε

.
Με κέντρο

και ακτίνα

κατασκευάζουμε κύκλο που τέμνει την

στο εσωτερικό του σημείο

, αφού η γωνία

είναι οξεία. Το τρίγωνο

είναι ισοσκελές με

άρα και

, οπότε τα τρίγωνα

είναι ίσα, άρα

.
Οπότε προσδιορίσαμε τη θέση του

.
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Πέμ Δεκ 14, 2017 11:13 pm
από Ορέστης Λιγνός

- point S.png (24.01 KiB) Προβλήθηκε 1967 φορές
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Πέμ Δεκ 14, 2017 11:17 pm
από Doloros
Παντού και πάντοτε τα νιάτα είναι ασυναγώνιστα !
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Πέμ Δεκ 14, 2017 11:30 pm
από Doloros

- Διαγωνισμός ομορφιάς_new.png (32.19 KiB) Προβλήθηκε 1955 φορές
Η κάθετη στο

επί την

τέμνει τον κύκλο

στο

. Το ημικύκλιο διαμέτρου

τέμνει την

ακόμα στο

Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Παρ Δεκ 15, 2017 7:36 pm
από george visvikis
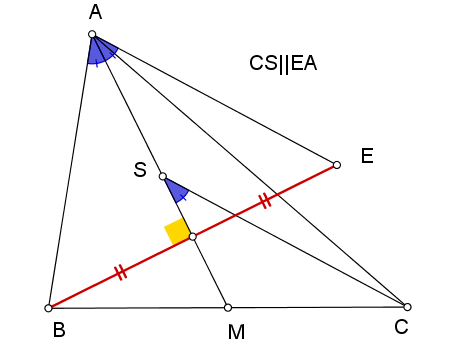
- Beauty star.png (14.38 KiB) Προβλήθηκε 1894 φορές
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Παρ Δεκ 15, 2017 8:14 pm
από KARKAR

- Διαγωνισμός ομορφιάς.png (10.6 KiB) Προβλήθηκε 1884 φορές
Παίρνω :

, τέλος ...
Ολιγόλογη και μυστηριώδης , κερδίζει το στέμμα , το οποίο δεν επιστρέφεται .
Επιτάχυνα κάπως την παρουσίαση της λύσης μου , επειδή ήθελα πολύ
αυτή τη νίκη και στην πίστα άρχιζαν να εμφανίζονται κι άλλες επικίνδυνα
όμορφες ! Δεν νομίζω ότι θα αμφισβητηθεί η απόφαση της κριτικής επιτροπής 
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Παρ Δεκ 15, 2017 8:17 pm
από Ανδρέας Πούλος
Επιδιώκω το βραβείο απλότητας.
Αν η επιτροπή είναι "κρητική" π.χ. Βαρβεράκης και Παντερής (που είναι και συνονόματοι), τότε το βραβείο το έχω στο τσεπάκι.

Ονομάζω β το μέτρο της γωνίας

.
Αν δοθούν δύο γωνίες με μέτρο φ και β, τότε είναι εύκολη η κατασκευή της γωνίας π-2φ-β, (επίπεδο Α Γυμνασίου).
Άρα, κατασκευάζω γωνία

με μέτρο π-2φ-β.
Τότε όπως φαίνεται στο συνημμένο σχήμα η γωνία

έχει μέτρο φ.
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Παρ Δεκ 15, 2017 8:58 pm
από Γιώργος Ρίζος
Γιώργος Ρίζος έγραψε: ↑Πέμ Δεκ 14, 2017 9:16 pm
Με κέντρο

και ακτίνα

κατασκευάζουμε κύκλο που τέμνει την

στο εσωτερικό του σημείο

, αφού η γωνία

είναι οξεία.
Απολογούμαι, συμπληρώνω: "Που τέμνει την

σε εσωτερικό σημείο

αν
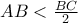
".
Πράγματι, αν

το πρόβλημα δεν έχει λύση.

- 15-12-2017 Γεωμετρία.png (52.79 KiB) Προβλήθηκε 1862 φορές
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Παρ Δεκ 15, 2017 9:39 pm
από KARKAR

- Διαγωνισμός ομορφιάς.png (19.77 KiB) Προβλήθηκε 1858 φορές
Επειδή ( ως επιτροπή ) έγινα δέκτης πολλών παραπόνων για μεροληψία προς μία
ανεπαρκή λύση , αναρτώ ένα ακόμη σχήμα , ελπίζοντας να ατονήσουν οι διαμαρτυρίες

Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Παρ Δεκ 15, 2017 10:43 pm
από Ορέστης Λιγνός
Θανάση συνέχισε να είσαι δίκαιος, αντικειμενικός, αμερόληπτος, αδέκαστος, απροκατάληπτος.
Ετσι μαθαίνουμε από μικροί ότι στη Ελλάδα ΠΑΝΤΑ υπάρχει ένα παρασκήνιο !!!
Υ.Γ. Θέλω να αγιάσω αλλά δεν με αφήνουν !!
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Παρ Δεκ 15, 2017 11:35 pm
από Ανδρέας Πούλος
Για να μη χάσω το "βραβείο".

Πρέπει να ισχύει 2φ + β < 180.
Υποθέτω αυτή παρατήρηση είναι ισοδύναμη με αυτή του Γιώργου Ρίζου για τη διερεύνηση της λύσης.
Πάντως, για άλλη μια φορά αποδεικνύεται ότι μια απλή άσκηση μπορεί να έχει ενδιαφέρον από την άποψη της μάθησης και της διδασκαλίας.
Τώρα, που το ξαναείδα, θα μπορούσε να γραφεί στην εκφώνηση, ότι το σημείο

ανήνει στον φορέα της διαμέσου,
οπότε μπορεί να βρίσκεται και εκτός του τριγώνου,
Έτσι, λύνεται το μειονέκτημα που επεσήμανε ο Γιώργος Ρίζος.
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 1:01 am
από Μιχάλης Τσουρακάκης
KARKAR έγραψε: ↑Πέμ Δεκ 14, 2017 8:12 pm
Διαγωνισμός ομορφιάς.pngΠάνω στη διάμεσο

τριγώνου

, καλούμαστε να εντοπίσουμε σημείο

,
έτσι ώστε :

. Κερδίζει η ομορφότερη λύση . Αλλά τα κριτήρια επιλογής , καθώς
και η σύνθεση της κριτικής επιτροπής δεν προαναγγέλλονται για ευνόητους λόγους .
Στις πανέμορφες λύσεις που προηγήθηκαν προσθέτω μια ακόμη
Με

συμμετρικό του
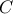
ως προς

είναι

,

κι επειδή
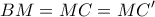
θα είναι

παραλ/μμο.
Άρα

.Η τομή του
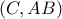
με την

δίνει τη θέση του


- D.O.png (11.92 KiB) Προβλήθηκε 1809 φορές
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 1:01 pm
από george visvikis

- Beauty star.II.png (17.18 KiB) Προβλήθηκε 1768 φορές

Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 1:27 pm
από KARKAR
Κύριοι , όπως προείπαμε το στέμμα δεν επιστρέφεται , όσο και να προσπαθήσετε

Είναι αλήθεια πάντως , ότι η επιτροπή εντυπωσιάστηκε από κάποιες υποψήφιες , κυρίως
δε από εκείνη του Ορέστη αλλά - είπαμε - το που θα δοθεί ο τίτλος , ήταν προαποφασισμένο

Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 1:49 pm
από Μιχάλης Νάννος

- shape.png (38.3 KiB) Προβλήθηκε 1761 φορές

συμμετρικό του

ως προς

…
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 3:00 pm
από Διονύσιος Αδαμόπουλος
KARKAR έγραψε: ↑Πέμ Δεκ 14, 2017 8:12 pm
Διαγωνισμός ομορφιάς.pngΠάνω στη διάμεσο

τριγώνου

, καλούμαστε να εντοπίσουμε σημείο

,
έτσι ώστε :

. Κερδίζει η ομορφότερη λύση . Αλλά τα κριτήρια επιλογής , καθώς
και η σύνθεση της κριτικής επιτροπής δεν προαναγγέλλονται για ευνόητους λόγους .
Χωρίς επιπλέον γραμμές...
Έστω

σημείο στην

ώστε

Επειδή η

είναι διάμεσος έχουμε:
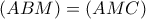
και
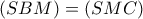
, επομένως

Είναι γνωστό (και προκύπτει εύκολα) ότι σε δύο τρίγωνα που έχουν μια γωνία ίση ή παραπληρωματική τότε ο λόγος των εμβαδών τους είναι ίσος με το λόγο των γινομένων των προσκείμενων στη γωνία πλευρών. Επομένως από τα τρίγωνα

και

έχουμε:

Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 3:18 pm
από KARKAR
Τι γίνεται ρε παιδιά , Βενεζουέλα καταντήσαμε !
Είναι γνωστό ότι η Βενεζουέλα "παράγει" το μεγαλύτερο ποσοστό καλλονών παγκοσμίως ...
Re: Διαγωνισμός ομορφιάς
Δημοσιεύτηκε: Σάβ Δεκ 16, 2017 4:26 pm
από Μιχάλης Νάννος

- shape2.png (23.55 KiB) Προβλήθηκε 1723 φορές

μεσοκάθετος της

,

και αποδεσμευόμαστε απ’ το να είναι η

διάμεσος…
 τριγώνου
τριγώνου  , καλούμαστε να εντοπίσουμε σημείο
, καλούμαστε να εντοπίσουμε σημείο  ,
, . Κερδίζει η ομορφότερη λύση . Αλλά τα κριτήρια επιλογής , καθώς
. Κερδίζει η ομορφότερη λύση . Αλλά τα κριτήρια επιλογής , καθώς  τριγώνου
τριγώνου  , καλούμαστε να εντοπίσουμε σημείο
, καλούμαστε να εντοπίσουμε σημείο  ,
, . Κερδίζει η ομορφότερη λύση . Αλλά τα κριτήρια επιλογής , καθώς
. Κερδίζει η ομορφότερη λύση . Αλλά τα κριτήρια επιλογής , καθώς  το σημείο τομής της
το σημείο τομής της  .
.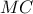 τέμνει στο
τέμνει στο  την κάθετο επί την
την κάθετο επί την  στο σημείο του
στο σημείο του  .
. τέμνει , εν γένει , την
τέμνει , εν γένει , την  έχουμε
έχουμε  και
και  .
. , είναι
, είναι 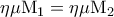 οπότε
οπότε  .
. και ακτίνα
και ακτίνα  κατασκευάζουμε κύκλο που τέμνει την
κατασκευάζουμε κύκλο που τέμνει την  είναι οξεία. Το τρίγωνο
είναι οξεία. Το τρίγωνο  είναι ισοσκελές με
είναι ισοσκελές με  άρα και
άρα και  , οπότε τα τρίγωνα
, οπότε τα τρίγωνα  είναι ίσα, άρα
είναι ίσα, άρα  .
.  επί την
επί την  τέμνει τον κύκλο
τέμνει τον κύκλο  στο
στο  . Το ημικύκλιο διαμέτρου
. Το ημικύκλιο διαμέτρου  τέμνει την
τέμνει την  , τέλος ...
, τέλος ... .
. με μέτρο π-2φ-β.
με μέτρο π-2φ-β. έχει μέτρο φ.
έχει μέτρο φ.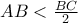 ".
". το πρόβλημα δεν έχει λύση.
το πρόβλημα δεν έχει λύση.  συμμετρικό του
συμμετρικό του 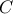 ως προς
ως προς  είναι
είναι  ,
,
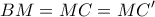 θα είναι
θα είναι  παραλ/μμο.
παραλ/μμο. .Η τομή του
.Η τομή του 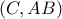 με την
με την 

 συμμετρικό του
συμμετρικό του  ως προς
ως προς  …
…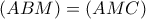 και
και 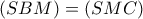 , επομένως
, επομένως 
 και
και  έχουμε:
έχουμε:
 μεσοκάθετος της
μεσοκάθετος της  και αποδεσμευόμαστε απ’ το να είναι η
και αποδεσμευόμαστε απ’ το να είναι η